Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 4

Произведение напряжения и тока есть мощность:

,                                                      (1.3)

измеряемая в ваттах (Вт).

Электрическая энергия, измеряемая в джоулях, определяется как интеграл

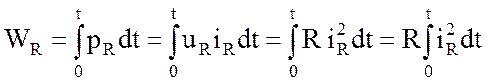.                      (1.4)

Индуктивность L, измеряемая в генри (Гн), представляет собой идеализированный элемент электрической цепи, способный накапливать энергию магнитного поля.

Переменный ток i_L наводит переменный магнитный поток Ф, который, в свою очередь, обусловливает появление ЭДС самоиндукции

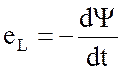,                                                      (1.5)

где  – потокосцепление, измеряемое, как и магнитный поток Ф, в веберах (Вб).

Для катушки, например, имеющей w витков, потокосцепление и магнитный поток  связаны соотношением:

.                                                       (1.6)

Связь между потокосцеплением и током определяется формулой

.                                                           (1.7)

В линейной электрической цепи L = const, поэтому подстановка (1.7) в (1.5) приводит к формуле:

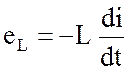.                                                    (1.8)

Падение напряжения на индуктивности u_L равно по величине ЭДС самоиндукцииe_L и противоположно по знаку, поэтому

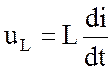.                                                       (1.9)

Произведение  также трактуется как мощность. Интеграл от этой величины представляет собой энергию магнитного поля в индуктивности:

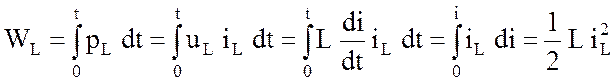.                      (1.10)

Емкость С измеряется в фарадах () и рассматривается как идеализированный элемент электрической цепи, накапливающий энергию электрического поля.

В качестве исходного здесь можно принять соотношение между зарядом q и напряжением u_C:

,                                                        (1.11)

где емкость С выступает как коэффициент пропорциональности между зарядом и напряжением. Единица измерения заряда – кулон (Кл).

Емкостный ток i_C, как количество заряда в единицу времени, определяется формулой

.

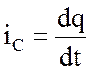При выполнении условия С = const c учетом (1.11) приходим к выражению

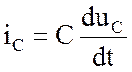.                                                (1.12)

Как и в предыдущих случаях, мощность выражается произведением , а энергия электрического поля:

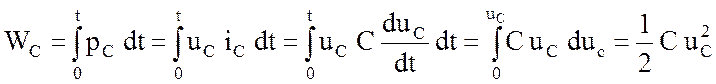.                  (1.13)

Взаимная индуктивность М, как параметр, присутствует в системах контуров или катушек, связанных между собой через магнитное поле.

На рис.1.3 изображена система двух магнитно- или индуктивно связанных катушек. Ток i₁ протекает по виткам первой катушки. Вторая катушка разомкнута и расположена в магнитном поле первой катушки.

Часть магнитного потока первой катушки , обозначенная на рис.1.3 как , проходит через сечение витков второй катушки, или, как говорят, сцеплена с витками второй катушки.

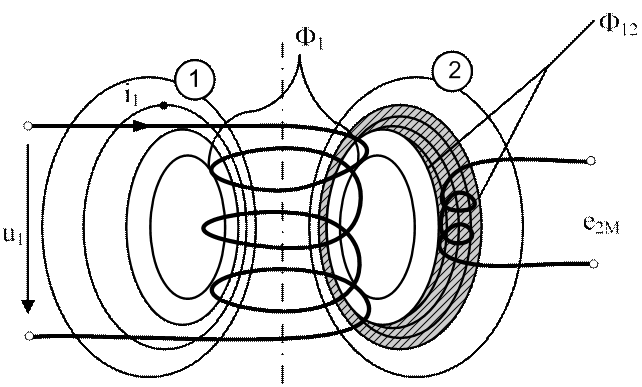
Рис. 1.3. Магнитное поле в системе двух катушек

Магнитному потоку  соответствует потокосцепление , которое с током первой катушки связано соотношением

.                                                     (1.14)

Потокосцепление  называют потокосцеплением взаимной индукции. Взаимная индуктивность М выступает как коэффициент пропорциональности между потокосцеплением  и обусловливающим его током i₁.

Магнитный поток взаимной индукции  наводит во второй катушке ЭДС взаимной индукции

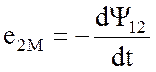,                                                 (1.15)

которая при М = const записывается как

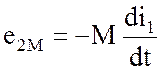.                                                (1.16)

Если токи имеют место в обеих катушках, то взаимная магнитная связь будет двухсторонней, т.е. ЭДС взаимной индукции будут наводиться и в первой и во второй катушках. При этом:

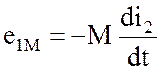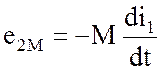;                 ,                 (1.17)

где e_1M и  e_2M – соответственно ЭДС взаимной индукции первой и второй катушек.

1.2.2.  Активные элементы электрических цепей

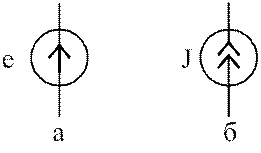
Рис. 1.4. Активные элементы:

а – источник напряжения (ЭДС); б – источник тока

Источник напряжения (ЭДС). На схемах он обозначается, как показано на рис.1.4,а. Это идеализированный элемент электрической цепи. Его внутреннее сопротивление принимается равным нулю, что обусловливает независимость ЭДС е от значения тока такого источника. Теоретически ток может изменяться от нуля до бесконечности, поэтому источник ЭДС является источником бесконечной мощности.