Схема с параллельным соединением элементов (рис.3.12, а) требует привлечения понятий комплексных проводимостей.
Уравнение для мгновенных значений записывается по первому закону Кирхгофа:
![]() .
.
или
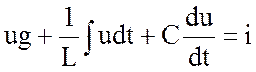 , (3.48)
, (3.48)
где
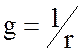 .
.
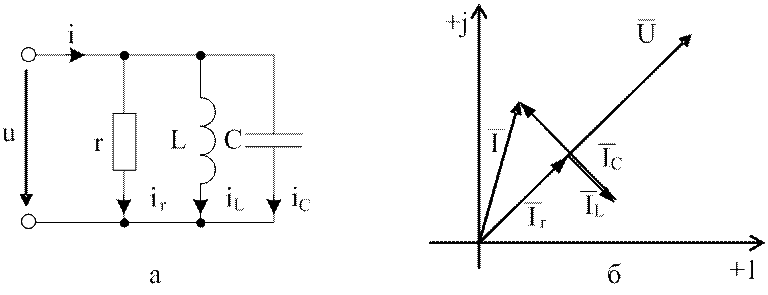
Рис.3.12. Электрическая цепь с параллельным соединением r, L и С
Уравнение в комплексной форме:
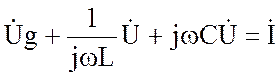 . (3.49)
. (3.49)
Векторная диаграмма токов показана на рис. 3.12, б.
Этапы преобразования полученного уравнения:
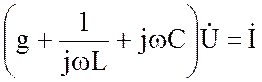 ;
;
 ;
;
![]() ;
;
![]() ;
;
![]() . (3.50)
. (3.50)
Здесь появились новые величины:
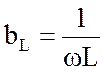 – индуктивная
проводимость;
– индуктивная
проводимость;
![]() – емкостная
проводимость;
– емкостная
проводимость;
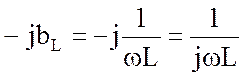 –
индуктивная проводимость в комплексной форме;
–
индуктивная проводимость в комплексной форме;
![]() – емкостная
проводимость в комплексной форме;
– емкостная
проводимость в комплексной форме;
![]() –
реактивная проводимость;
–
реактивная проводимость;
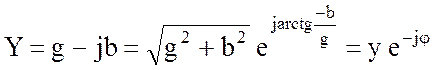 - комплексная
проводимость;
- комплексная
проводимость;
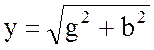 – полная
проводимость как модуль комплексной проводимости.
– полная
проводимость как модуль комплексной проводимости.
Любая комплексная проводимость выступает как величина обратная комплексному сопротивлению. Для отдельных элементов:
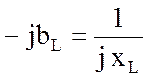 ;
; 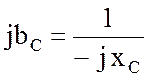 (3.51)
(3.51)
В общем случае:
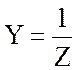 ;
; 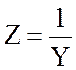 (3.52)
(3.52)
Формулы (3.52) бывают полезны в тех случаях, когда требуется преобразовать последовательные схемы в параллельные и наоборот. Предположим, что требуется схему рис.3.13,а преобразовать в схему рис.3.13,б.
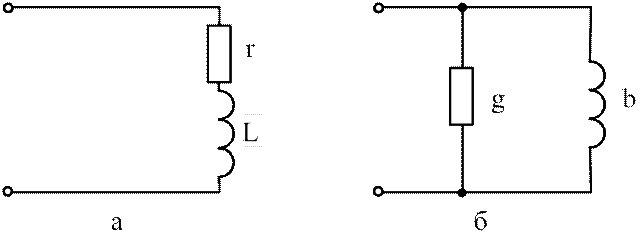
Рис.3.13. Преобразование схем:
а – с последовательным соединением; б – с параллельным соединением
Комплексное сопротивление первой схемы записывается в форме
![]() .
.
Комплексная проводимость записывается как величина, обратная Z:
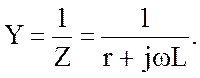
Умножая числитель и знаменатель дроби на комплекс, сопряжённый знаменателю, получаем
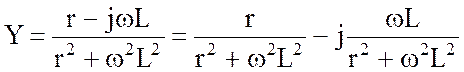
В итоге значения проводимостей схемы рис.3.13,б равны:
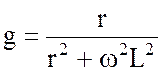 ;
; 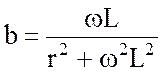
Реализацию обратного перехода можно осуществить путем преобразования общей комплексной проводимости схемы рис.3.13,б в комплексное сопротивление согласно формулам:
![]() ;
;
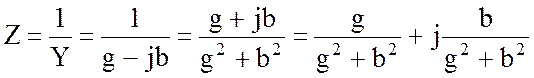
откуда
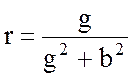 ;
; 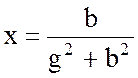 ;
; 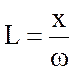 .
.
3.6. Особенности применения комплексного метода для исследования
разветвленных электрических цепей
Положительной стороной комплексного метода является то обстоятельство, что операции с комплексными напряжениями, токами, сопротивлениями и проводимостями осуществляются по тем же основным правилам, что и в случае цепей постоянного тока.
Законы Кирхгофа для цепей постоянного тока формируются алгебраическим суммированием составляющих – токов при формировании уравнений по первому закону Кирхгофа, а также ЭДС и падений напряжений при составлении уравнений по второму закону Кирхгофа.
В случае цепей переменного тока алгебраическое суммирование в действительной области применимо только для мгновенных значений, как это сделано при составлении уравнений (3.17), (3.44), (3.48). Действующие и амплитудные значения напряжений и токов суммируются только геометрически, на что указывают все приведенные ранее векторные диаграммы.
В комплексной форме алгебраические операции можно производить практически со всеми, встречающимися при расчете электрических цепей величинами: комплексными амплитудами, комплексными действующими значениями, комплексными сопротивлениями и проводимостями. Нужно лишь правильно применять правила действий с комплексными числами.
Рассмотрим схему, изображённую на рисунке 3.14,а.
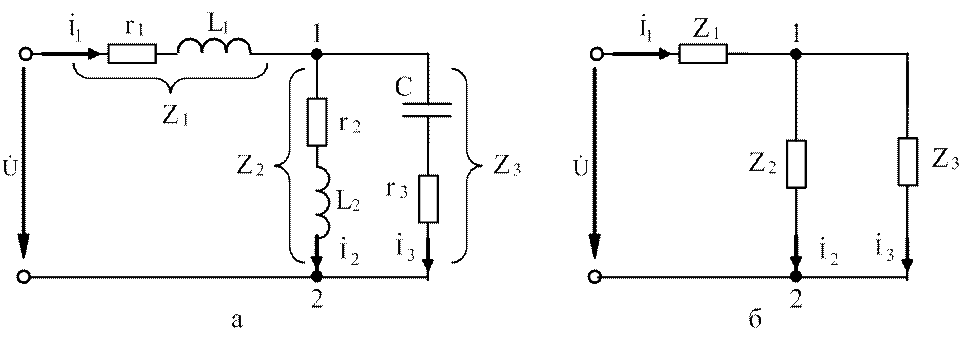
Рис.3.14. Расчетная схема:
а – заданная; б - упрощенная
Параметры элементов схемы заданы. Задано также входное
напряжение ![]()
Ставится задача определить токи ветвей. Расчет проводится по комплексным действующим значениям.
Сначала необходимо определить входное комплексное
сопротивление ![]() . Это можно сделать по исходной
схеме рис.3.14,а. Но если есть затруднения, то можно перейти к упрощенной схеме,
изображенной на рис.3.14,б, введя обозначения
. Это можно сделать по исходной
схеме рис.3.14,а. Но если есть затруднения, то можно перейти к упрощенной схеме,
изображенной на рис.3.14,б, введя обозначения
![]() ;
;
![]() ;
;
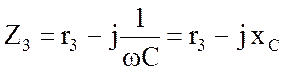 .
.
Получили в итоге последовательно-параллельное соединение трех комплексных сопротивлений, для которого
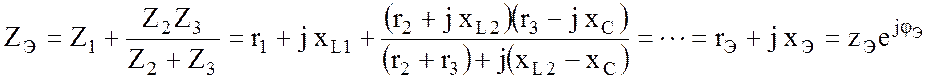 (3.53)
(3.53)
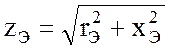 – полное
(входное) сопротивление схемы;
– полное
(входное) сопротивление схемы;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.