Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 19

На щитках электрических машин и аппаратов переменного тока в качестве номинальных, как правило, указываются действующие значения напряжений и токов. Измерительные приборы электромагнитной и других систем измеряют действующие значения соответствующих величин.

При расчетах электрических цепей синусоидального тока широко используются понятия комплексных действующих значений или комплексов напряжений и токов. Последние, как и действующие значения (3.42), отличаются от комплексных  амплитуд в    раз:

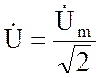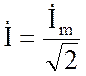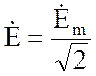,   ,          .                          (3.43)

3.5. Комплексные соотношения для трехэлементных

электрических цепей

В качестве первого представителя рассмотрим схему с последовательным соединением элементов r, L и С (см. рис. 3.11,а).

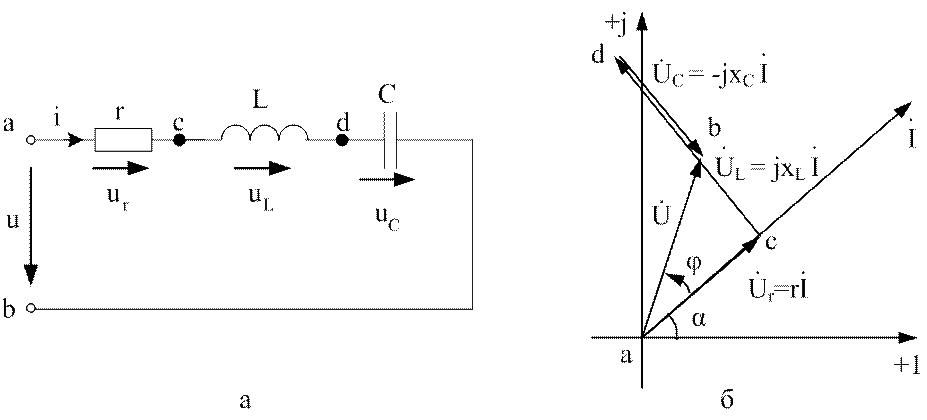
Рис.3.11. Электрическая цепь с последовательным соединением r, L, C

Эта схема одноконтурная, поэтому записываем уравнение для мгновенных значений по второму закону Кирхгофа:

или

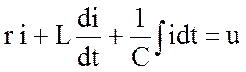.                                   (3.44)

Пусть

;

.

Условимся использовать запись по комплексным действующим значениям, которые в данном случае имеют вид:

,    .

Уравнению (3.44) в комплексной форме соответствует уравнение

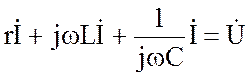,                                            (3.45)

которое преобразуется в следующей последовательности:

;

;

;

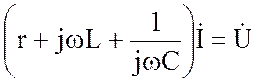,                                                     (3.47)

где   – реактивное сопротивление;

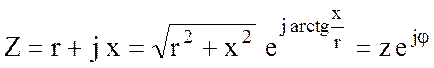 - комплексное сопротивление цепи;

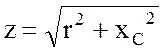 - полное сопротивление или модуль комплексного сопротивления;

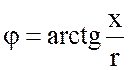 – аргумент комплексного сопротивления, представляющий собой угол сдвига фаз между входным напряжением и током.

Установленные здесь закономерности имеют общий характер и сводятся к следующему:

- индуктивное и емкостное сопротивления в состав общего реактивного сопротивления входят  с разными знаками (индуктивное – с плюсом, емкостное – с минусом);

- модуль комплексного сопротивления есть полное сопротивление;

- аргументом комплексного сопротивления всегда является  угол сдвига фаз между соответствующими напряжением и током.

Результатом решения является комплексное действующее значение тока (комплекс тока)

,

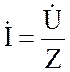по которому легко записывается мгновенное значение.

Векторная диаграмма (см. рис.3.11,б) построена в масштабах действующих значений тока и напряжений (модулей комплексов).

Общей величиной для всех элементов является ток I. Поэтому вектор тока на данной диаграмме является исходным или базовым.

Векторы падений напряжения ориентированы относительно вектора тока с учетом фазовых соотношений для элементов r, L и С: в сопротивлении r напряжение и ток совпадают по фазе; в индуктивности напряжение опережает ток на 90⁰; в емкости напряжение отстает от тока на 90⁰.

Направление обхода контура выбрано по часовой стрелке. Векторы падений напряжения на векторной диаграмме соответствуют расположению элементов на схеме, т.е. последовательно из точки  а  отложены векторы U_r, U_L, и U_C. Геометрическая сумма этих векторов равна приложенному напряжению U.

Векторные диаграммы такого типа называются топографическими векторными диаграммами. Главная их особенность – соответствие расположения векторов падений напряжений расположению элементов на схеме.

Направление обхода контура при построении векторной диаграммы может быть противоположным, т.е. против часовой стрелки. В таком случае расположение векторов падений напряжений будет противоположным, поскольку начальной точкой для построения будет точка b.

Векторная диаграмма (рис.3.11,б) соответствует случаю, когда индуктивное сопротивление  превышает емкостное 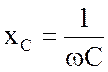, поэтому падение напряжения на индуктивности , больше падения напряжения ,  угол    положителен, напряжение по фазе опережает ток и относительно входных зажимов схема воспринимается как активно-индуктивная. При выполнении условия   вектор  будет меньше вектора  и схема относительно входных зажимов будет восприниматься как активно-емкостная, поскольку вектор напряжения  окажется отстающим по отношению к току . Возможен и частный случай, когда  и . Угол сдвига фаз в этом случае равен нулю и схема попадает в режим резонанса напряжений.