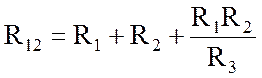 ;
; 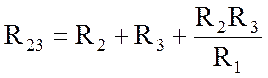 ;
; 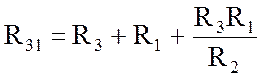 . (2.8)
. (2.8)
Чередование индексов в правых частях формул позволяет легко установить закономерность в их формировании.
2.6.2. Преобразование параллельного соединения ветвей
с источниками ЭДС
Упрощение задачи по исследованию электрической цепи достигается заменой участка с параллельно соединенными ветвями одной ветвью с эквивалентными параметрами. Пусть, например, требуется участок с тремя параллельными ветвями (рис.2.12,а) заменить одной ветвью с двумя элементами RЭ и ЕЭ (рис.2.12,б). Задача сводится к нахождению числовых значений эквивалентной ЭДС и эквивалентного сопротивления RЭ.
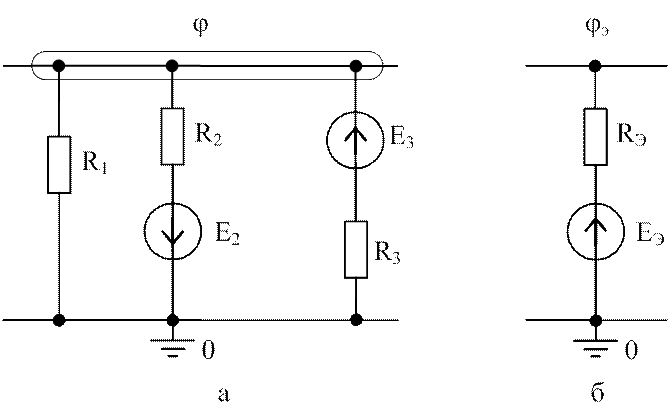
Рис. 2.12. Преобразование параллельных ветвей:
а – исходная расчетная схема; б – двухэлементная эквивалентная схема.
Применяем метод узловых потенциалов. Нижний узел левой
схемы принимается базисным (![]() = 0). Потенциал
верхнего узла подлежит определению.
= 0). Потенциал
верхнего узла подлежит определению.
Обе схемы будут эквивалентными при равенстве
потенциалов ![]()
![]() .
.
Единственное уравнение по методу узловых потенциалов в данном случае имеет вид:
![]() ,
,
откуда
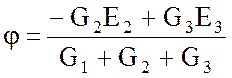
или в общей форме записи
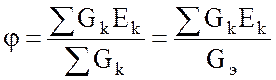 , (2.9)
, (2.9)
где
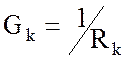 .
.
Аналогичное уравнение можно записать и для потенциала ![]() эквивалентной схемы:
эквивалентной схемы:
![]() ,
, 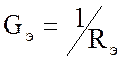 ,
,
откуда
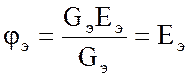 . (2.10)
. (2.10)
В силу условия эквивалентности ![]() в
конечном итоге получаем соотношения для преобразования:
в
конечном итоге получаем соотношения для преобразования:
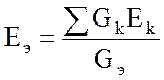 ;
; ![]() ;
; 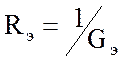 . (2.11)
. (2.11)
Эквивалентная проводимость GЭ является суммой проводимостей ветвей. Применительно к схеме рис. 2.12,а это есть величина
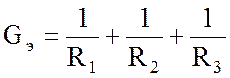 .
.
Произведение GkEk в числителе формулы (2.11) имеет знак плюс, если направление ЭДС ветви совпадает с выбранным направлением эквивалентной ЭДС ЕЭ:
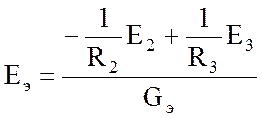 .
.
Формулы (2.11) применяются при любом числе параллельных ветвей.
2.7. Примеры расчета электрических цепей постоянного тока
2.7.1. Применение законов Кирхгофа
Условие задачи. Составить уравнения по законам Кирхгофа для определения токов ветвей в схеме, приведенной на рис.2.13.
Дано: Е1, Е2, Е3, J, R1, R2, R3, R4, R5, R6.
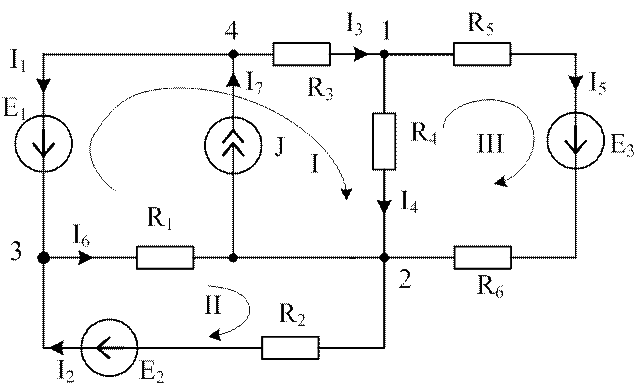
Рис. 2.13. Схема, демонстрирующая применение законов Кирхгофа
Решение.
В схеме (см. рис.2.13) семь ветвей, четыре узла и четыре независимых контура. Ток I7 известен (I7 = J), поэтому неизвестных токов в схеме шесть. Для расчета токов данным методом необходимо составить систему из шести уравнений, в которой три уравнения должны быть записаны по первому закону Кирхгофа и три – по второму. Выбираем независимые контуры так, чтобы ветвь с источником тока не вошла ни в один из контуров.
Выбираем произвольно направления токов в ветвях и направления обхода контуров (например, по часовой стрелке). Записываем систему из шести уравнений, совместное решение которых дает искомые токи:
![]() узел 1:
узел 1: ![]() ;
;
узел
2: ![]() ;
;
узел
3: ![]() ;
;
контур
I: ![]() ;
;
контур
II: ![]() ;
;
контур
III: ![]() .
.
Ток источника тока, как следует из приведенных соотношений, входит только в уравнения по первому закону Кирхгофа.
2.7.2. Метод контурных токов
Условие задачи. Определить токи ветвей в схеме, приведенной на рис.2.14.
Дано: Е1 = 10 В, Е2 = 5 В, Е3 = 4 В, J = 2 А, R1 = 5 Ом,
R2 = 5 Ом, R3 = 1 Ом, R4 = 4 Ом, R5 = 2 Ом, R6 = 3 Ом.
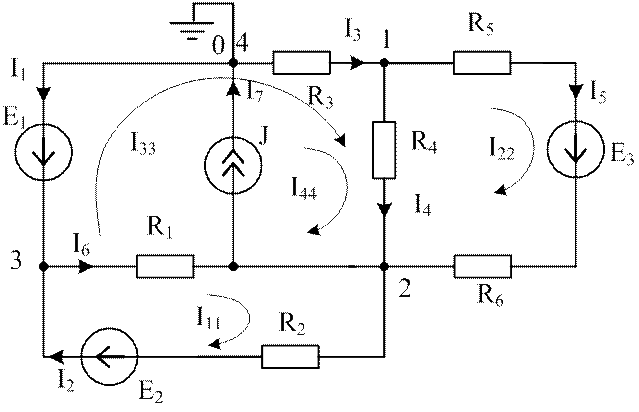
Рис. 2.14. Схема для применения метода контурных токов
Решение.
Выбираем независимые контуры так, чтобы ветвь с источником тока не оказалась общей для контуров. Выбираем произвольно направления четырех контурных токов, причем один из них известен: I44 = J.
В общем виде составляем систему уравнений относительно трех неизвестных контурных токов:
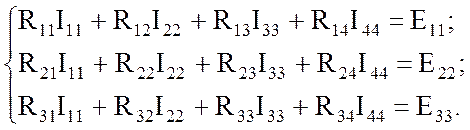
где
![]() ; R11 = 10 Ом;
; R11 = 10 Ом;
![]() ; R22 = 9 Ом;
; R22 = 9 Ом;
![]() ; R33 = 10 Ом;
; R33 = 10 Ом;
![]() ;
; ![]() ,
, ![]() Ом;
Ом;
![]() ;
; ![]() ;
; ![]() Ом;
Ом;
![]() ;
; ![]() Ом;
Ом; ![]()
![]() Ом;
Ом;
![]() ; E11 = 5 В, E22 = E3; E22 = 4 В E33 = -E1; E33 = –10 В.
; E11 = 5 В, E22 = E3; E22 = 4 В E33 = -E1; E33 = –10 В.
После подстановки система уравнений принимает вид:
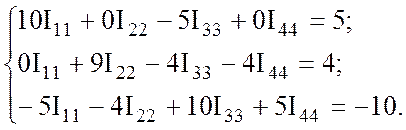
После подстановки ![]() A получаем:
A получаем:
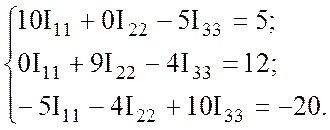
По правилу Крамера
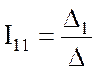 ;
; 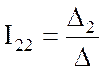 ;
; 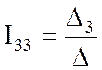 .
.
где 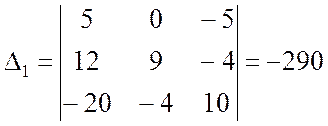 ;
; 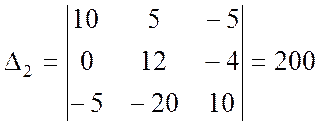 ;
;
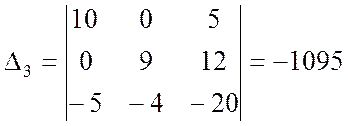 ;
; 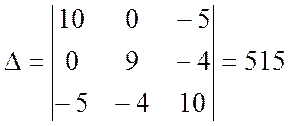 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.