![]() , (4.17)
, (4.17)
решение которого
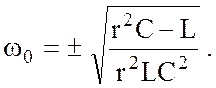 (4.18)
(4.18)
Резонансная частота – реальный физический параметр. Поэтому положительный ответ о наличии резонанса напряжений дает только положительное, действительное значение корня. Следовательно, окончательно используем значение
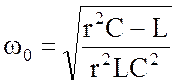 , (4.19)
, (4.19)
которое
указывает, что резонанс в исследуемой схеме возможен при выполнении условия ![]() . Если это
условие не выполняется, то числитель подкоренного выражения будет
отрицательным, а корень, соответственно, мнимым.
. Если это
условие не выполняется, то числитель подкоренного выражения будет
отрицательным, а корень, соответственно, мнимым.
Рассмотрим схему рис.4.6,б при числовых значениях
параметров: r = 100 Ом, L = 0,01 Гн, ![]() Ф. Расчетная схема представлена на рис.4.7.
Ф. Расчетная схема представлена на рис.4.7.
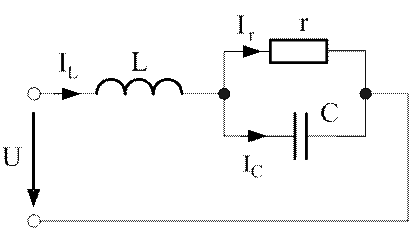
Рис.4.7. Расчетная схема
Резонансная частота определяется по формуле (4.19)
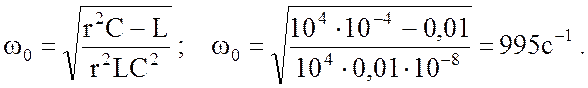
Получили действительное положительное значение, следовательно, при данной частоте и заданных параметрах r, L, C в схеме имеет место резонанс напряжений. Чтобы разобраться в его особенностях, необходимо провести расчет токов и построить векторную диаграмму.
Входное сопротивление при резонансной частоте ![]() согласно
(4.15) равно:
согласно
(4.15) равно:
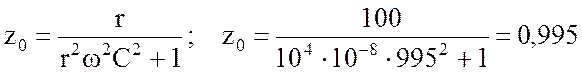 Ом.
Ом.
Резонансные значения токов:
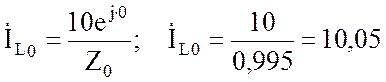 А;
А;
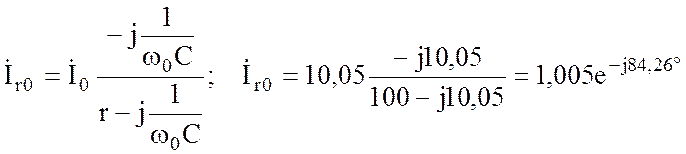 ;
;
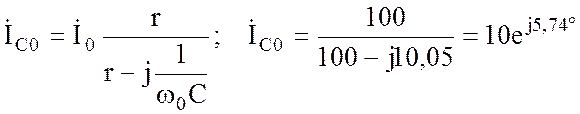 .
.
Падения напряжений:
![]() ;
;
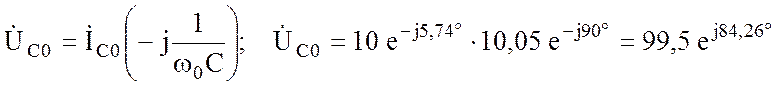 .
.
По полученным данным на рис.4.8 построена векторная диаграмма, характеризующая резонансный режим в схеме рис.4.7.
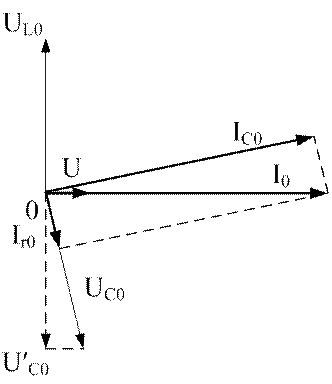
Рис.4.8. Диаграммы напряжений и токов при резонансе
Особенности приведенной векторной диаграммы сводится к следующему.
Напряжение U и ток IL0 совпадают по фазе.
Реактивные напряжения UL0 и UC0 в отличие от схем рис.3.11,а и рис.4.6,а не находятся в противофазе, т.е. сдвинуты одно относительно другого на угол, не равный 1800. Поэтому полная компенсация этих напряжений невозможна. В противофазе находятся напряжение UL0 и составляющая U′C0 напряжения UC0. Кроме того, имеет место равенство между UL0 и U′C0. В результате можно сказать, что условие резонанса напряжений в данной схеме обеспечивается напряжениями UL0 и U′C0.
Наконец, можно отметить, что рассматриваемая векторная диаграмма соответствует схеме с достаточно высокой добротностью:
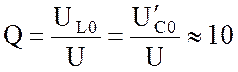 ,
,
т.е. напряжения на реактивных элемента L и C примерно в 10 раз превышают приложенное напряжение.
В схемах рис.4.9 индуктивность и емкость находятся в параллельных ветвях, поэтому, как уже показано для схемы рис.4.7,а, в этих схемах возможен резонанс токов.
Обратимся к схеме рис.4.9,б и, учитывая ее структуру, запишем выражение для комплексной проводимости:
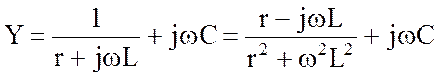 . (4.20)
. (4.20)
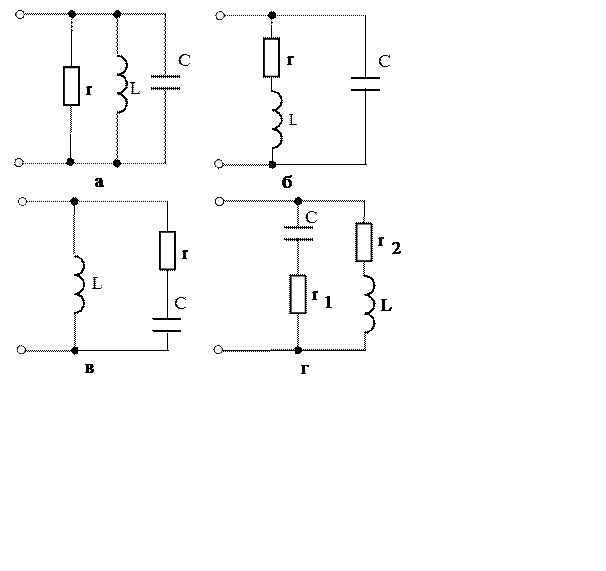
Рис. 4.9. Схемы, в которых возможен резонанс токов
Разделяя действительную и мнимую части (4.20) в конечном итоге приходим к уравнению
![]() , (4.21)
, (4.21)
корень которого
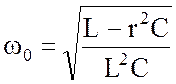 (4.22)
(4.22)
указывает
на возможность резонанса токов при выполнении условия ![]() .
.
Можно было бы убедиться, что использование в качестве исходного выражения формулы для комплексного сопротивления
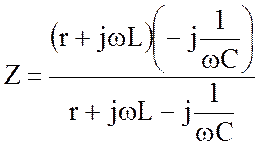
приводит к тому же уравнению (4.21) относительно резонансной частоты и к тому же значению корня этого уравнения (4.22). Но преобразования при этом более сложные, поэтому в схемах с параллельными ветвями предпочтение отдается комплексной проводимости.
Для выявления особенностей исследования резонанса
токов в схеме рис.4.9,б снова обратимся к числовым значениям параметров: r = 50 Ом,
L = 0,05 Гн, ![]() Ф, U = 100В. Расчетная схема изображена на рис.4.10. Расчет приводится
в комплексной форме.
Ф, U = 100В. Расчетная схема изображена на рис.4.10. Расчет приводится
в комплексной форме.
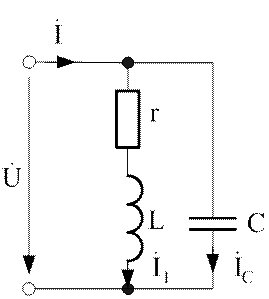
Рис.4.10. Расчетная схема
Резонансная частота по формуле (4.22):
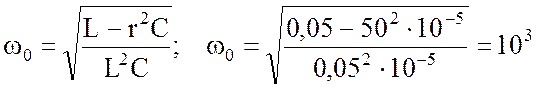 с-1
с-1
Входная проводимость схемы при частоте ![]() согласно формуле (4.20):
согласно формуле (4.20):
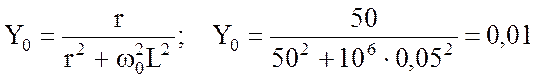 См
См
Резонансные значения токов:
![]() А;
А;
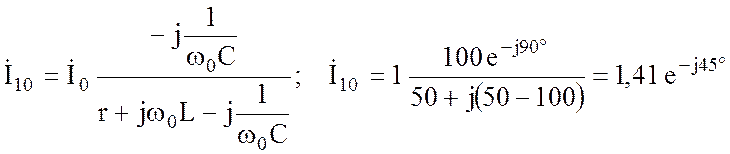 ;
;
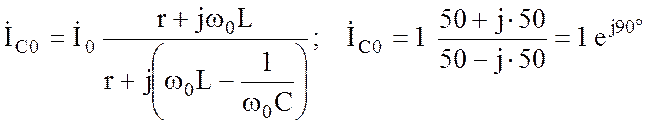 .
.
Падения напряжений:
![]()
![]() .
.
Соответствующая расчету векторная диаграмма приведена на рис.4.11.
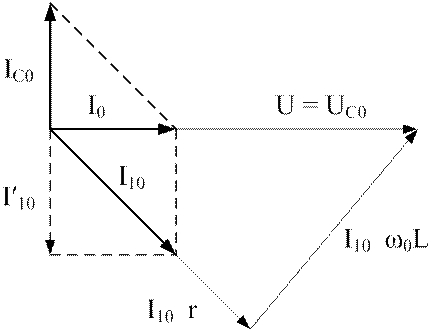
Рис.4.11. Диаграммы токов и напряжений при резонансе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.