Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 26

где  – эквивалентная индуктивность схемы;

           – эквивалентное сопротивление схемы.

Встречное включение (см. рис.3.24,б) характеризует следующее уравнение

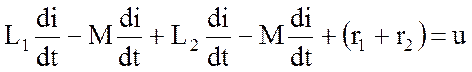,                        (3.75)

где  дополнительные падения напряжения 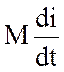, обусловленные взаимной магнитной связью катушек, вычитаются.

Поэтому после преобразований получаем:

;

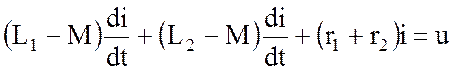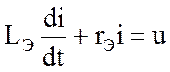  ,                                             (3.76)

где ; .

В первом случае, как следует из (3.74), взаимная индуктивность М обусловливает увеличение эквивалентной индуктивности. В данном случае эквивалентная индуктивность уменьшается, но остается величиной положительной в любых условиях.

Разности  и  в (3.76) могут быть как положительными, так и отрицательными, но не одновременно.

Уравнения (3.73) и (3.76) можно записать в комплексной форме, например, относительно комплексных действующих значений напряжений и тока:

для согласного включения

;

для встречного включения

.                       (3.77)

Степень магнитной связи между двумя катушками характеризует параметр

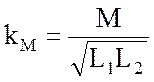,                                                 (3.78)

который называют коэффициентом магнитной связи. Этот коэффициент в зависимости от условий имеет значения в диапазоне от нуля до единицы. Нулевое значение k_м достигается в случаях, когда оси катушек взаимно перпендикулярны. Максимальное значение, близкое к единице, может быть получено при так называемой бифилярной намотке, когда намотка обеих катушек осуществляется соприкасающейся парой проводов.

3.10.2. Магнитно-связанные цепи без электрической связи

Такой тип электрических цепей характерен для электротехнических устройств – трансформаторов, которые предназначены для преобразования параметров напряжения и тока. Исключительное большинство реально используемых трансформаторов выполняются на ферромагнитных сердечниках и представляют собой нелинейные устройства. Находят также применение в специальных случаях трансформаторы без ферромагнитных сердечников - «воздушные трансформаторы». Эти устройства являются линейными и поэтому являются предметом обсуждения в данном разделе.

Схема простейшего двухобмоточного воздушного трансформатора изображена на рис.3.26.

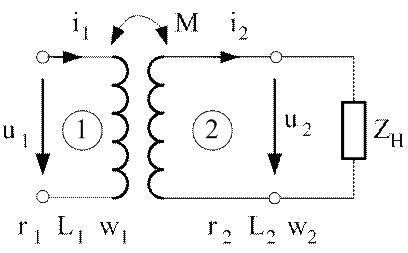
Рис.3.26. Воздушный трансформатор

Трансформатор имеет первичную и вторичную обмотки. Первичная обмотка подключается к источнику, вторичная обмотка питает нагрузку Z_н .

Все параметры первичной обмотки имеют индекс единицу, вторичной обмотки – двойку.

Электрическое соединение между первичной и вторичной обмотками отсутствует. Энергия во вторичный контур передается через изменяющееся во времени магнитное поле.

Схема рассматриваемого трансформатора двухконтурная, поэтому можно записать два уравнения по второму закону Кирхгофа:

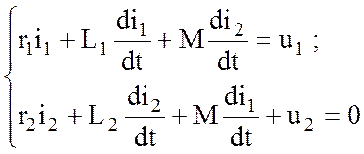
или

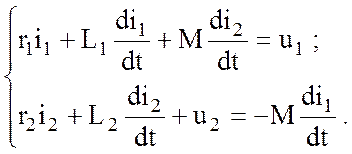                                  (3.79)

Здесь величина – 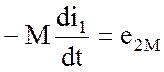 представляет собой ЭДС взаимной индукции, которая током первичной обмотки i₁ наводится во вторичной обмотке. Именно эта ЭДС обусловливает ток i₂ во вторичной обмотке трансформатора и нагрузке Z_н.

Составляющая 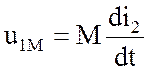 в первом уравнении (3.79) является падением напряжения, которое компенсирует ЭДС взаимной индукции 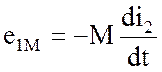, наводимой током вторичной обмотки i₂ в первичной обмотке. Наличие ЭДС e_1M и e_2M характеризуют двухстороннюю магнитную связь в схеме воздушного трансформатора.

В режиме холостого хода, когда вторичный контур разомкнут, ток  и система (3.79) приобретает вид

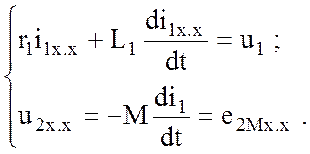                                        (3.80)

В этом режиме магнитная связь односторонняя, поскольку магнитный поток вторичной обмотки отсутствует.

Уравнения (3.79) в комплексной форме имеют вид:

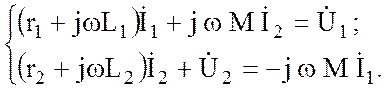                             (3.81)

Решение этих уравнений позволяет определить токи первичной и вторичной обмоток и исследовать режимы трансформатора в полном диапазоне изменения параметров, т.е. от режима холостого хода до режима короткого замыкания (Z_н = 0).