Сделано такое предположение для удобства математического исследования режимов электрических цепей: любые изменения параметров подключенной к источнику цепи, не влияют на его ЭДС.
Реальные источники напряжения обладают конечными внутренними сопротивлениями. На рис. 1.5,а приведены так называемые внешние характеристики идеального источника ЭДС и реального источника напряжения для случая, когда величины E, I и Rвн являются постоянными в том смысле, что изменения тока осуществляются только за счет параметров цепи нагрузки.
Из рис. 1.5,а следует, что ЭДС Е, т.е. ЭДС идеализированного источника, не зависит от величины тока, а зависимость напряжения от тока падающая, поскольку с увеличением тока возрастает вычитаемое из ЭДС падение напряжения на внутреннем сопротивлении Rвн.
На схемах замещения реальные источники напряжения чаще всего представляются двухэлементной схемой, как показано на рис.1.5,б.
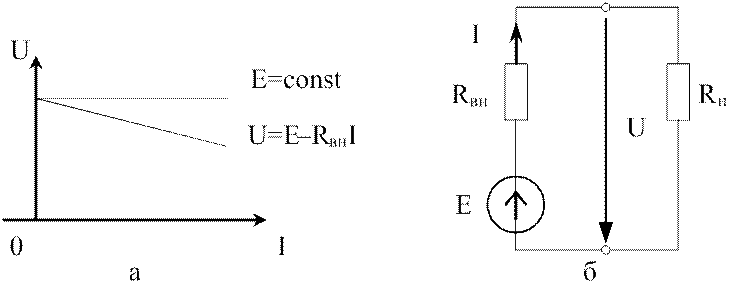
Рис.1.5. Источник напряжения:
а – внешние характеристики; б – схема замещения
Источник тока (см. рис.1.4.б) также идеализированное понятие. Внутреннее его сопротивление принято бесконечным, что позволяет обеспечить независимость значения тока J от режима питаемой источником цепи. При изменении параметров цепи нагрузки источника тока, значение J остается заданным, а изменяется напряжение на его зажимах. Поскольку теоретически это напряжение может изменяться от нуля до бесконечности, то источник тока, как и источник ЭДС, является источником бесконечной мощности.
В реальной жизни в основном приходится иметь дело с источниками напряжения. К источникам тока могут приближаться реальные источники с большими внутренними сопротивлениями, которые встречаются в области электроники и вычислительной техники.
1.3. Режимы электрических цепей
Режимы электрических цепей подразделяются на установившиеся и переходные (нестационарные).
В установившемся режиме линейная электрическая цепь находится в состоянии равновесия, когда токи, падения напряжения на элементах ее неизменны или являются периодическими функциями времени. При этом обязательно выполняется энергетический баланс между источниками и пассивными элементами цепи.
Переходные процессы возникают при изменении параметров цепи, когда электрическая цепь переходит из одного установившегося состояния в другое, например, при включении и выключении цепей, при подключении и отключении отдельных ветвей, скачкообразном изменении каких-либо сопротивлений, индуктивностей и емкостей, в различных аварийных режимах и пр.
Установившиеся режимы математически описываются алгебраическими уравнениями или соотношениями с действительными или комплексными коэффициентами. Математическим аппаратом исследования переходных процессов в линейных электрических цепях с сосредоточенными параметрами являются дифференциальные уравнения с постоянными коэффициентами.
Предметом изучения в рамках данной дисциплины является только установившиеся режимы. При этом рассматриваются, как уже указывалось выше, два класса цепей: цепи с постоянными токами и напряжениями («Цепи постоянного тока») и цепи с периодическими синусоидальными токами и напряжениями («Цепи синусоидального тока»).
Математический аппарат цепей постоянного тока удобен для изучения основных методов анализа электрических цепей, находящих применение при исследовании и других классов электрических цепей. Наиболее простую трактовку в этом разделе получают и фундаментальные законы Кирхгофа, сфера применения которых выходит далеко за рамки цепей постоянного тока.
Важность изучения методов исследования цепей синусоидального тока с одной стороны, заключается в том, что здесь закладываются теоретические основы понимания процессов, характеризующих режимы систем переменного тока в энергетике, электромеханике и других областях; с другой стороны, закладываемая в этом разделе теоретическая база, необходима для понимания в дальнейшем различных частотных представлений и методов, широко применяемых во многих отраслях техники.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.