Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 29

Векторная диаграмма, изображенная на рис.3.11,б, в режиме резонанса напряжений превращается в диаграмму рис.4.1.

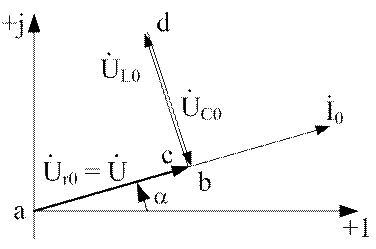
Рис.4.1. Резонанс напряжений

На этой диаграмме напряжения  и  равны, поэтому падение напряжения на сопротивлении r равно приложенному напряжению U. Последнее по фазе совпадает с током I и цепь относительно входных зажимов воспринимается как чисто активная.

Такой эффект является следствием взаимной компенсации напряжений  и , но не их исчезновения. Как и в любом другом режиме, процессы в индуктивности связаны с магнитным полем, а в емкости – с электрическим. В индуктивности периодические изменения энергии магнитного поля определяются формулой (1.10):

.

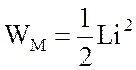В емкости энергия изменяется согласно (1.13):

.

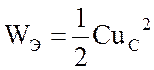В произвольном режиме энергии W_M и W_Э в любой момент отличаются по величине, т.е. не компенсируются. Преобладание той или иной из них определяет режим схемы в том смысле, что относительно входных зажимов цепь может восприниматься как активно-индуктивная или активно-емкостная. Векторная диаграмма рис.3.11,б отражает случай активно-индуктивной реакции цепи, поскольку на ней U_L > U_C и входное напряжение U опережает входной ток I. При резонансе (см. рис.3.32) напряжения U_L и U_C одинаковы. Соответственно одинаковы и периодические составляющие энергий W_M и W_Э, которые взаимно компенсируются. В итоге, на входных зажимах цепь воспринимается как активная, хотя каждый из элементов L и C сохраняют свои энергетические параметры как и падения напряжений U_L и U_C.

Реактивные сопротивления при резонансе имеют значения:

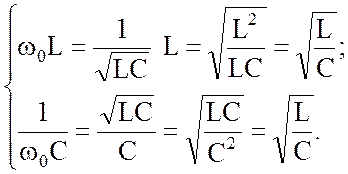
Величина 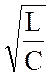 обозначается буквой  и называется характеристическим или волновым сопротивлением контура

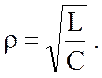                                                (4.4)

Отношение

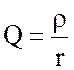                                                    (4.5)

есть величина, которая называется добротностью контура. Эта величина характеризует соотношение между реактивными и активным сопротивлениями в резонансном режиме. В такой же мере добротность характеризует и соотношение между напряжениями:

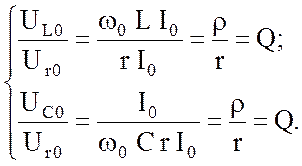                                                         (4.6)

Понятие добротности широко используется в теории фильтров, как один из основных параметров оценки их качества.

На рис.4.2 изображены две векторные диаграммы для резонансного режима.

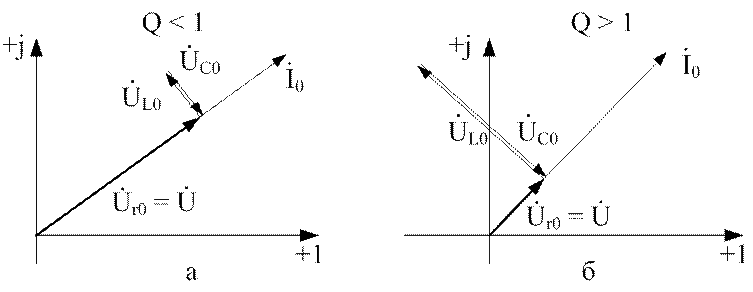
Рис.4.2. Резонанс напряжений:

а – Q < 1;  б – Q > 1

Первая диаграмма (рис.4.2,а) соответствует значению добротности Q < 1. Диаграмма рис.4.2, б характеризуется значением Q > 1. В первом случае реактивные напряжения U_L0 и U_C0 меньше входного напряжения, во втором – больше. Следовательно, добротность Q является числовой оценкой кратности напряжений. Например, если имеем значение Q = 2, то это означает, что

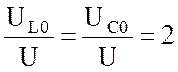
и падения напряжений на индуктивности и емкости в два раза превышают приложенное напряжение.

При исследовании резонансных свойств электрических цепей широко используются частотные характеристики, т.е. зависимости токов, напряжений и других физических величин от угловой частоты . При этом имеет распространение построение графиков в относительных координатах. При построении зависимости, например, тока от частоты в качестве независимой переменной вместо   берется относительная частота 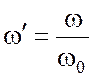, а вместо тока I – отношени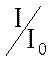е  где  и I₀ - соответственно резонансные значения частоты и тока. При таком подходе легче сравнивать характеристики, имеющие место при различных параметрах резонансного контура.

На рис.4.3. в относительных координатах воспроизведены кривые 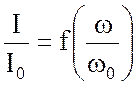 для двух значений добротностей Q₁ и Q₂ .

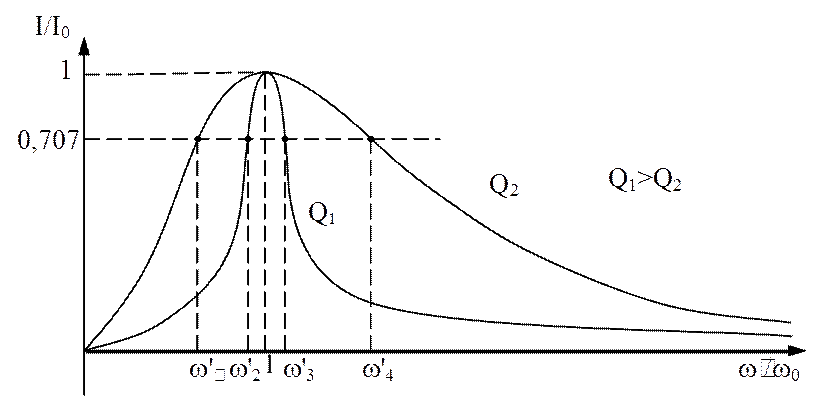
Рис.4.3. Характеристики резонанса в относительных координатах

Рассматриваемый последовательный резонансный контур обладает свойствами полосового фильтра. В определенной полосе частот его входное сопротивление мало и он обусловливает значения тока, приближающиеся к максимальному значению 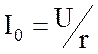. Такая полоса частот называется полосой пропускания или полосой прозрачности фильтра.