Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 8

Запишем уравнения по первому закону Кирхгофа, предварительно выбрав направления токов в ветвях:

узел 1:                        ;                                  (2.3)

узел 2:                       .

Выразим токи ветвей через потенциалы узлов:

;

;

;       ;

;          ;        

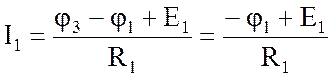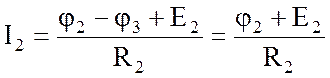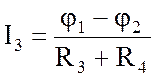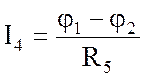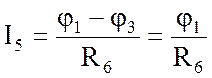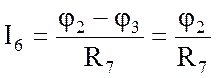и подставим в систему (2.3):

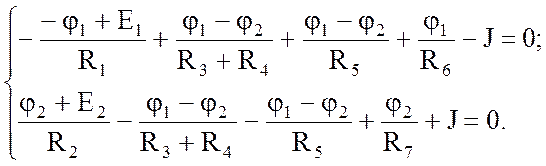
После группировки получим:

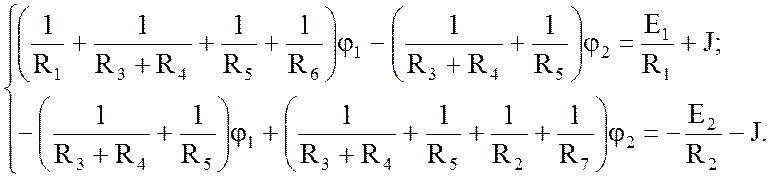
В общем виде:

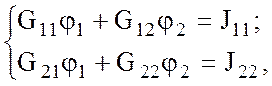                                           (2.4)

где G₁₁, G₂₂ – собственные (узловые) проводимости узлов 1 и 2, каждая из которых равна сумме проводимостей ветвей, сходящихся в данном узле;

G₁₂ = G₂₁ – общая проводимость – взятая со знаком «минус» сумма проводимостей ветвей, соединяющих узлы 1 и 2 (проводимость ветви, содержащей источник тока, равна нулю);

J₁₁, J₂₂ – задающие (узловые) токи узлов 1 и 2, каждый из которых равен алгебраической сумме произведений ЭДС на проводимости ветвей, в которых они находятся (рассматриваются ветви, подключенные к данному узлу), и алгебраической сумме токов источника тока, подключенных к данному узлу. Знаки слагаемых: «плюс» - если направление ЭДС (источника тока) к узлу, «минус» - если направление ЭДС (источника тока) от узла.

2.3.1.  Последовательность определения токов ветвей методом узловых потенциалов

1. Записывается система уравнений в общем виде. Число уравнений системы на единицу меньше числа узлов схемы. Если в схеме содержится ветвь с источником ЭДС без сопротивлений (рис. 2.5), то . Приняв , получим .

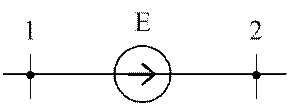
Рис. 2.5. Ветвь схемы с источником ЭДС

2. Определяются коэффициенты при неизвестных – собственные и общие проводимости, а также задающие токи узлов.

3.  Рассчитываются потенциалы узлов.

4.  Выбираются направления токов ветвей.

5.  Определяются токи ветвей.

При выборе способа расчета той или иной цепи, как правило, лучшим считается тот, который требует решения меньшего количества уравнений.

Метод узловых потенциалов с этой точки зрения обладает преимуществами в тех случаях, когда число узлов схемы меньше количества контуров. В качестве примера, подтверждающего это положение, приведена схема рис.2.6.

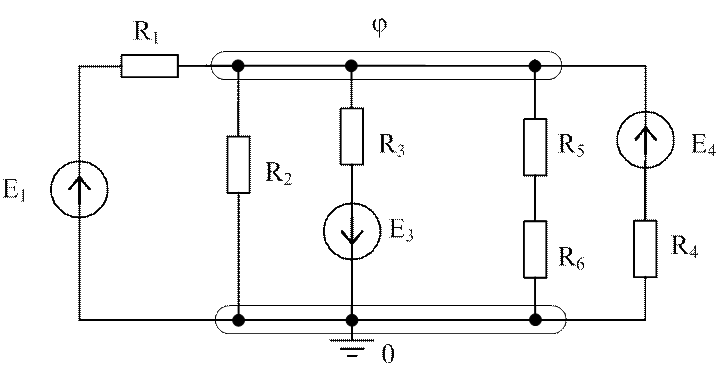
Рис.2.6. Схема электрической цепи с двумя узлами

Данная схема имеет четыре независимых контура и два узла. Применяя непосредственно законы Кирхгофа, пришлось бы решать систему из пяти уравнений. Метод контурных токов требует решения четырех уравнений. По методу узловых потенциалов достаточно решить только одно уравнение для определения потенциала верхнего узла :

,

где  ;

.

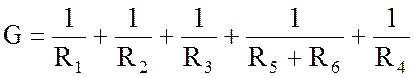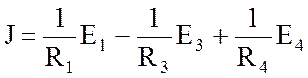Поскольку потенциал нижнего (базисного) узла равен нулю, то потенциал  численно равен напряжению на каждой из параллельных ветвей. Поэтому нахождение значений токов ветвей представляет весьма простую задачу.

2.4. Метод активного двухполюсника (эквивалентного источника)

При расчетах линейных электрических цепей  возможна замена части цепи, содержащей источники ЭДС и тока, относительно зажимов выделенной ветви ab (рис.2.7,а) активным двухполюсником, состоящим из последовательно соединенных ЭДС и сопротивления. В этом случае указанную ветвь можно рассматривать как нагрузку эквивалентного источника с ЭДС Е_э и сопротивлением R_э.

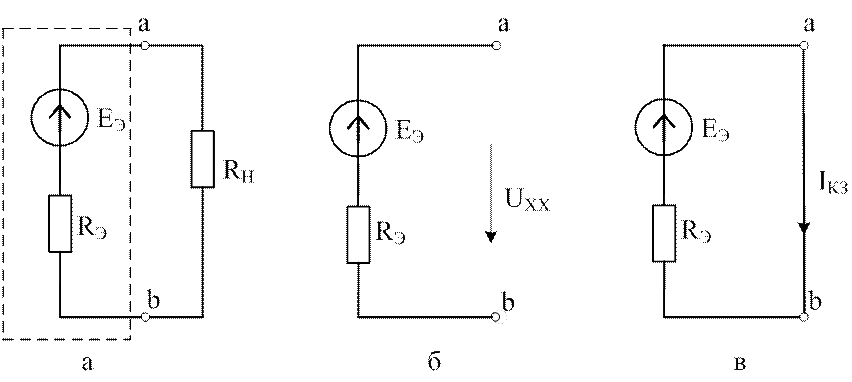
Рис. 2.7. Последовательность схем для метода эквивалентного источника

Эквивалентная ЭДС Е_э равна напряжению на зажимах аb при разомкнутой ветви R_н , т.е. напряжению холостого хода U_х.х.

Сопротивление R_э равно входному сопротивлению цепи относительно зажимов аb при разомкнутой ветви R_н. Источники при этом исключаются из схемы.

Эквивалентные параметры Е_э и R_э могут быть определены опытным путем из режимов холостого хода (рис. 2.7,б) и короткого замыкания (рис. 2.7,в):

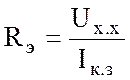;  .                                          (2.5)

Обратимся к схеме рис. 2.8,а и поставим задачу заменить ее простейшей эквивалентной схемой рис.2.8,б при условии неизменности тока I_Н в сопротивлении R_Н.

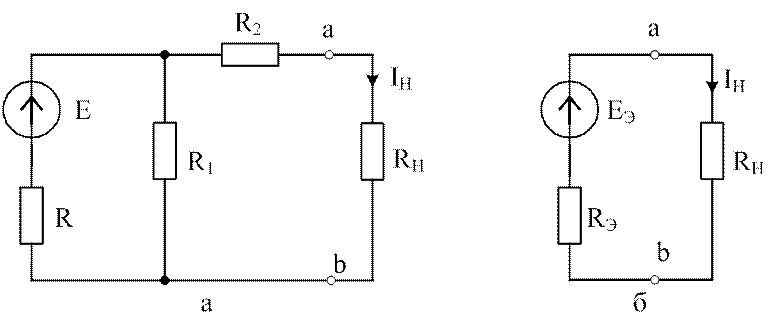
Рис. 2.8. Метод эквивалентного источника:

а – исходная расчетная схема; б – схема с эквивалентными параметрами

Эквивалентная ЭДС Е_Э определяется по схеме рис. 2.9.а.

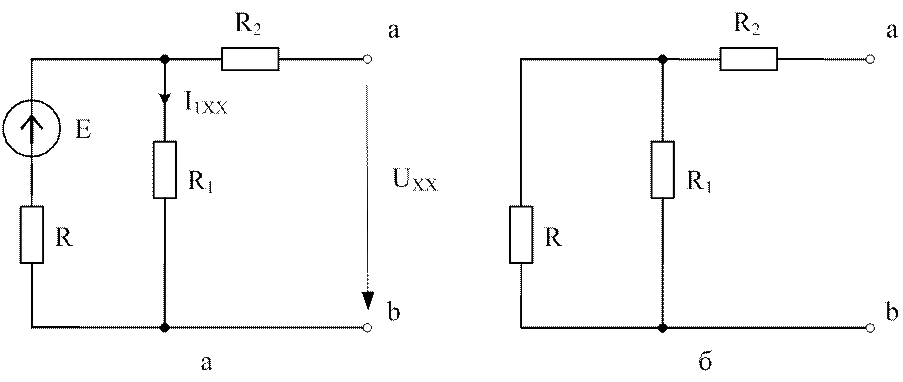
Рис. 2.9. Метод эквивалентного источника: