Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 17

Рис. 3.8. Напряжение и ток в цепи с r и l

Особенности построения векторной диаграммы: поскольку имеет место последовательное соединение элементов r и L, то вектор тока I_m отложен как исходный; относительно тока отложены векторы падений напряжений rI_m и x_LI_m; геометрическим сложением получен вектор входного напряжения U_m. Масштабы напряжения и тока выбраны независимыми.

Аналогичные преобразования для цепи r, C (см. рис.3.7,б) привели бы к следующему результату:

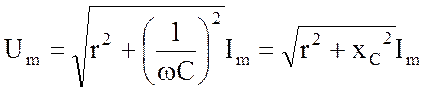                        (3.22)

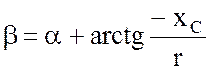                                                 (3.23)

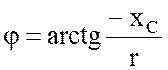                                                    (3.24)

Угол сдвига фаз в данном случае отрицателен и может принимать любое значение в диапазоне от нуля до  Следовательно, при любых соотношениях между r и x_с входное напряжение цепи отстает по фазе от тока.

Емкостное сопротивление, 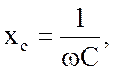 так же как и индуктивное, относится к разряду реактивных сопротивлений, поскольку значение этого сопротивления обусловливается обратимыми процессами изменения энергии электрического поля.

На рис.3.9,а приведена временная диаграмма для случая r = x_с, (). Этой диаграмме соответствует векторная диаграмма рис.3.9,б.

Выявленные фазовые соотношения между напряжениями и токами в индуктивности и емкости обусловлены разной физической природой магнитного и электрического полей, что находит выражение в следующих парах соотношений:

Рис.3.9. Напряжение и ток в цепи с r и c

- для индуктивности

;        ;

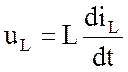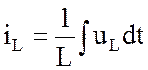- для емкости

;        .

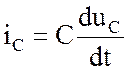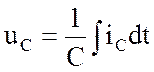Интегральной величиной в случае индуктивности является ток, а в емкости – напряжение. Именно эти величины являются запаздывающими по фазе при любых изменениях напряжений и токов во времени.

Установленные понятия:

-  r – активное сопротивление;

-  x_L, x_C – реактивные сопротивления;

- z – полное сопротивление

используются при исследовании любых цепей синусоидального тока.

3.3. Основы комплексного (символического) метода расчета

электрических цепей синусоидального тока

Используемые нами в предыдущем параграфе соотношения для мгновенных значений напряжений и токов неудобны для расчета сложных цепей, так как приводят к весьма громоздким выражениям, требующим большого объема преобразований и вычислений. Значительное упрощение расчетов достигается переходом к комплексным числам и соотношениям в комплексной форме.

Любое комплексное число, как известно, можно представить в различных формах:

 ,

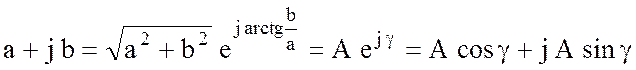где ; ; .

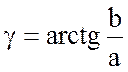В основу дальнейших рассуждений положим равенство:

 ,

которое может быть использовано и для комплексных функций времени.

На рис.3.10 изображен вектор, вращающийся с угловой скоростью    на комплексной плоскости.

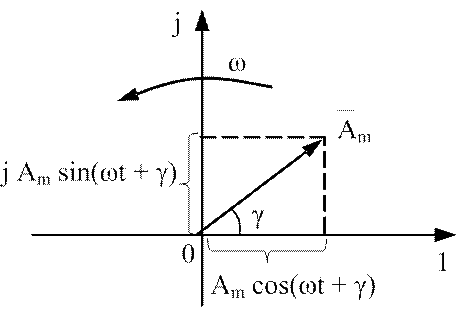
Рис.3.10. Вращающийся вектор на комплексной плоскости

Проекции вращающегося вектора на оси действительных и мнимых значений представляют собой гармонические функции, поэтому можно записать:

или

 ,                   (3.25)

где

.                                           (3.26)

Величину  называют комплексной амплитудой.

Дифференцирование и интегрирование (3.25) приводит к соотношениям:

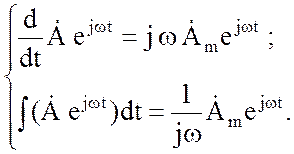                                                       (3.27)

Соотношение (3.25) обладает следующим свойством: по любой из трех составляющих этого выражения можно восстановить две другие. Угловая частота, как правило, бывает задана. Такими же свойствами обладают и выражения (3.27).

Можно также утверждать, что при известной частоте   полную информацию обо всех составляющих (3.25) имеет комплексная амплитуда (3.26).

Очевидны еще следующие свойства (3.25):

- суммированию комплексных функций слева соответствует суммирование комплексных функций справа;

- умножению левой части на постоянный множитель соответствует умножение правой части на тот же множитель.

Установленные свойства позволяют вести речь об однозначном соответствии между мнимой частью (3.25) слева и комплексной амплитудой справа:

  .                                        (3.28)