Уравнения трансформатора с ферромагнитным сердечником
формируются в несколько иной форме. Рассмотрим идеализированную модель двухобмоточного
трансформатора (см. рис.3.27), принимая условие ![]() , где
, где ![]() - абсолютная магнитная проницаемость сердечника.
- абсолютная магнитная проницаемость сердечника.
Магнитная проницаемость сердечника во много раз превышает магнитную проницаемость воздуха, поэтому магнитный поток в основном замыкается внутри сердечника и образуется составляющая Ф, называемая основным магнитным потоком; незначительная часть общего потока ответвляется в воздух.
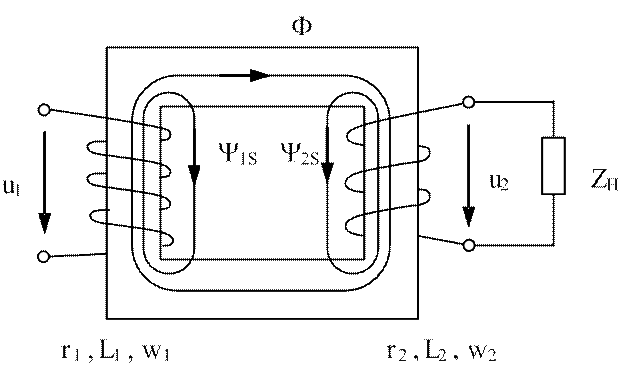
Рис.3.27. Двухобмоточный трансформатор
На рис.3.27 эта часть обозначена потокосцеплениями ![]() и
и ![]() . Поскольку
магнитная проницаемость воздуха величина постоянная (
. Поскольку
магнитная проницаемость воздуха величина постоянная (![]() ), то
справедливы соотношения:
), то
справедливы соотношения:
![]() и
и ![]() ,
,
где
![]() и
и ![]() -
индуктивности рассеяния первичной и вторичной обмоток.
-
индуктивности рассеяния первичной и вторичной обмоток.
С обеими обмотками связан основной магнитный поток Ф, поэтому он и определяет взаимную магнитную связь между обмотками.
Уравнения (3.79) для рассматриваемой модели приобретают следующий вид:
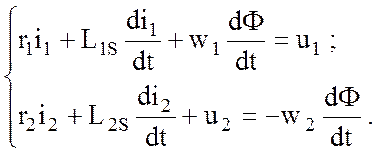 (3.82)
(3.82)
В этой системе
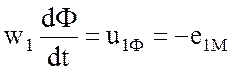 – падение
напряжения, компенсирующее ЭДС
– падение
напряжения, компенсирующее ЭДС ![]() , наводимую в первичной обмотке потоком Ф;
, наводимую в первичной обмотке потоком Ф;
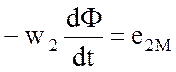 – ЭДС, наводимая потоком Ф во вторичной обмотке;
– ЭДС, наводимая потоком Ф во вторичной обмотке;
![]() ,
, ![]() – соответственно число витков первичной и
вторичной обмоток.
– соответственно число витков первичной и
вторичной обмоток.
Отношение ЭДС
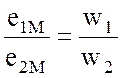
является одним из важнейших параметров применяемых трансформаторов и называется коэффициентом трансформации:
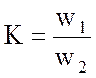 . (3.83)
. (3.83)
Приближенное значение коэффициента трансформации
определяется как отношение напряжений ![]() и
и ![]() .
.
3.10.3. Особенности расчета разветвленных цепей с
магнитно-связанными элементами
Рассмотрим особенности составления уравнений по законам Кирхгофа на примере схемы рис.3.28. Сложность состоит в том, что в отличие от обычных цепей, здесь на правило знаков, связанное с обходом контура, накладывается еще правило согласного и встречного включения. Поэтому рекомендуется следующая последовательность действий.
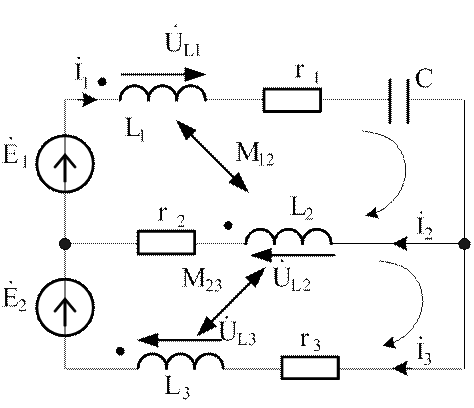
Рис.3.28. Разветвленная цепь с магнитно-связанными элементами
Сначала необходимо стрелками обозначить падения
напряжений ![]() ,
, ![]() ,
, ![]() на
индуктивностях согласно с направлениями токов ветвей. Значения этих напряжений
выражаются с применением правила определения согласного и встречного включения:
на
индуктивностях согласно с направлениями токов ветвей. Значения этих напряжений
выражаются с применением правила определения согласного и встречного включения:
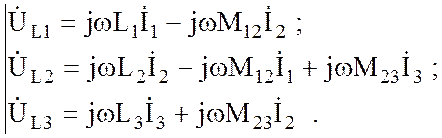 (3.84)
(3.84)
Затем составляется система уравнений для двух контуров и одного узла схемы:
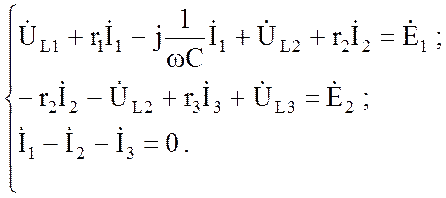 (3.85)
(3.85)
Подстановка значений напряжений в (3.85) приводит к конечной системе уравнений:
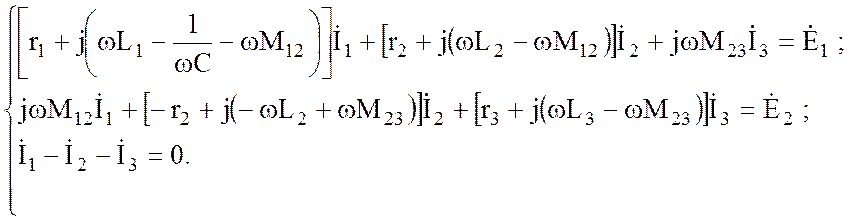 (3.86)
(3.86)
которая и подлежит решению.
В итоге видно, что система уравнений (3.85) составлена только с учетом правил, которые сформулированы ранее в разделе 2.1 при рассмотрении законов Кирхгофа. Разделение на отдельные этапы составления соотношений (3.84) и уравнений (3.85) позволяет избежать ошибок в знаках членов конечной системы уравнений (3.86).
Для решения подобных задач может быть применен и метод контурных токов. Но его реализация сложнее, так как требуется использовать дополнительные правила составления уравнений. Метод узловых потенциалов принципиально неприменим, поскольку его основу составляет зависимость тока ветви только от напряжения на зажимах этой же ветви. В данном случае этот принцип нарушается, так как из-за наличия магнитных связей ток ветви зависит от режимов и других ветвей.
3.10.4. Примеры расчета электрических цепей с магнитно-связанными элементами
Пример 1. В электрической цепи (см. рис.3.29) имеют место следующие параметры:
U = 5
В, ![]() Ом,
Ом, ![]() Ом,
Ом,
![]() Ом,
Ом, ![]() Ом,
Ом, ![]() Ом,
Ом, ![]() Ом.
Ом.
Требуется:
а) комплексным методом определить ток цепи;
б) построить векторную диаграмму.
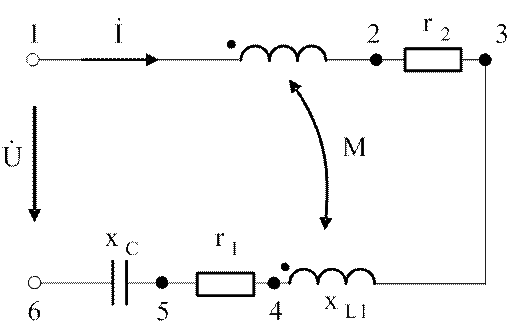
Рис.3.29. Электрическая цепь с магнитно-связанными элементами
Решение.
Расчетный ток входит в начало второй и конец первой катушки, следовательно, катушки включены встречно.
По второму закону Кирхгофа имеем:
![]()
или
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.