Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 15

Угловая частота  , частота  f  и период Т связаны соотношением:

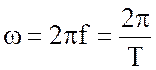.                                                (3.2)

На рис. 3.1,а построен временной график функции , а на рис. 3.1,б – соответствующая векторная диаграмма.

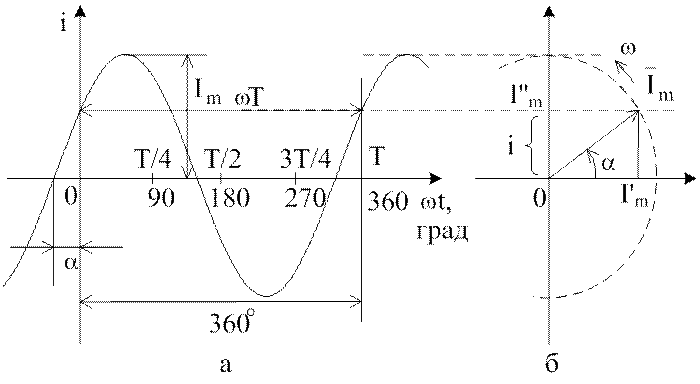
Рис. 3.1. Синусоидальная функция и ее представление вращающимся вектором

Проекция вращающегося против часовой стрелки с постоянной угловой скоростью    вектора  I_m  (см.рис. 3.1,б) на вертикальную ось изменяется во времени по синусоидальному закону. Поэтому любая синусоидальная функция (ток, напряжение, ЭДС) может быть изображена вектором. На рис. 3.1,б изображен вектор тока с проекциями  и .

На рис. 3.2,а кривые напряжения и тока совмещены на одной диаграмме. Начальным фазам соответствуют значения , поскольку в качестве независимой переменной взято время t.

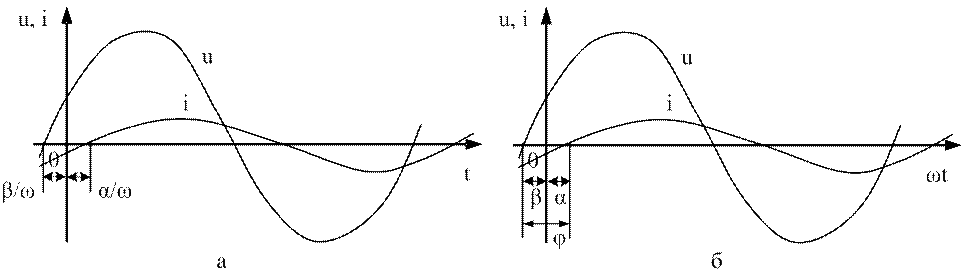
Рис. 3.2. Фазовые сдвиги

Из формулы (3.2) следует равенство . Для части периода, например,  t₁ по аналогии можно записать , откуда . Поэтому на рис. 3.2,а обозначены не начальные фазы  , а соответствующие им отрезки  .

Пользоваться подобными диаграммами неудобно, поэтому чаще вместо времени t в качестве независимой переменной используют произведение   (см. рис.3.2.,б). Тогда и появляются начальные фазы, измеряемые в угловых единицах.

На диаграмме рис.3.2,б отмечен еще один очень важный параметр, а именно, угол

,                                                   (3.3)

который называется углом сдвига фаз между напряжением и током.

Начало положительной полуволны напряжения находится левее начала координат. Поэтому начальная фаза    считается опережающей и   - положительно , при этом при t = 0 значение напряжения положительно (u(0) > 0).

Положительная полуволна тока начинается правее начала координат (запаздывает). Поэтому начальная фаза тока  определяется как запаздывающая или отстающая и на указанном рисунке она отрицательна (), при этом значение тока при t = 0 отрицательно (i(0) < 0).

3.2. Синусоидальные режимы простейших электрических цепей

В качестве простейших рассматриваются одноэлементные схемы r, L и C и двухэлементные – r, L и r, C.

Пусть в рассматриваемых случаях напряжение и ток описываются выражениями

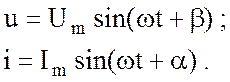                                                  (3.4)

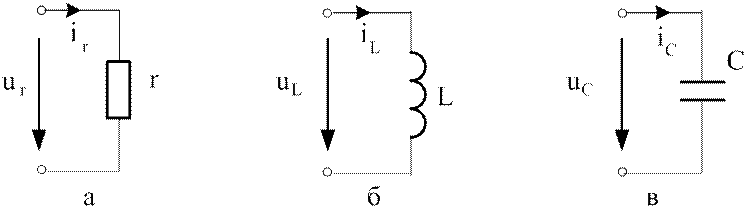
Рис.3.3. Одноэлементные схемы:

а – сопротивление; б – индуктивность; в – емкость

В сопротивлении r напряжение и ток подчинены закону Ома, поэтому

или после подстановки

.

Равенство выполняется, если отдельно равны амплитуды и начальные фазы левой и правой частей:

;                                                   (3.5)

.                                                              (3.6)

Равенство (3.5) показывает, что закон Ома в данном случае справедлив для амплитуд. Смысл равенства (3.6) состоит в том, что напряжение u_r и ток i_r совпадают по фазе.

На временной диаграмме (см. рис. 3.4,а) моменты перехода через нулевые значения совпадают у обеих кривых. На векторной диаграмме соответственно совпадают направления векторов напряжения и тока (см. рис. 3.4,б). Угол сдвига фаз между напряжением и током равен нулю ().

Векторы на рис.3.4,б соответствуют амплитудам напряжения и тока. Масштабы напряжения и тока при построении векторной диаграммы выбираются независимо.

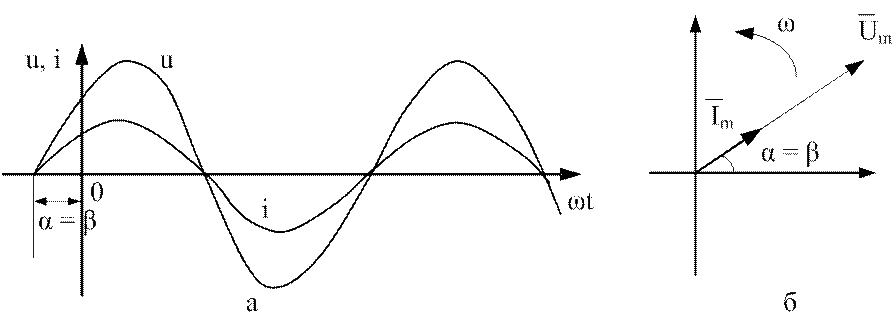
Рис. 3.4. Синусоидальные напряжения и ток:

а – временная диаграмма; б – векторная диаграмма

Соотношения (3.5) и (3.6) справедливы для каждого сопротивления в составе любой схемы замещения, независимо от ее структуры и количества элементов. Всегда в сопротивлении напряжение и ток совпадают по фазе (см.рис.3.4,а).

В индуктивности L(см.рис.3.3,б) напряжение и ток в соответствии с (1.9), связаны формулой

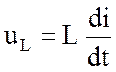    .                                                  (3.7)

Подстановка (3.4) в (3.7) дает:

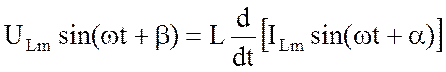
или

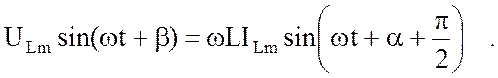
откуда следуют равенства

;                                                (3.8)

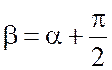.                                                       (3.9)

Величина   имеет размерность сопротивления, обозначается как х_L и называется индуктивным сопротивлением: