I11 = –0,563 А; I22 = 0,388 А; I33 = –2,126 А; I44 = 2 А.
В итоге токи ветвей:
I1 = –I33; I1 = 2,126 A;
I2 = I11; I2 = –0,563 A;
I3 = I33 + I44; I3 = –0,126 A;
I4 = I33 + I44 – I22; I4 = –0,514 A;
I5 = I22; I5 = 0,388 A;
I6 = I11 – I33; I6 = 1,563 A;
I7 = I44; I7 = 2 A.
Знак «минус» у токов I2, I3 и I4 указывает на то, что в действительности эти токи имеют направления, противоположные указанным на схеме.
2.7.3. Метод узловых потенциалов
Условие задачи. Определить токи ветвей в схеме (см. рис.2.14), используя данные предыдущей задачи.
Решение.
Заземляем узел 4 (![]() 4
= 0). Кроме того, ветвь между узлами 3 и 4 содержит только источник ЭДС,
следовательно, независимо от величины протекающего тока I1, величина
4
= 0). Кроме того, ветвь между узлами 3 и 4 содержит только источник ЭДС,
следовательно, независимо от величины протекающего тока I1, величина ![]() также известна:
также известна: ![]() = Е1 (направление Е1 к
узлу 3). Таким образом, в задаче неизвестными являются потенциалы двух узлов -
= Е1 (направление Е1 к
узлу 3). Таким образом, в задаче неизвестными являются потенциалы двух узлов - ![]() и достаточно составить систему из двух
уравнений
и достаточно составить систему из двух
уравнений
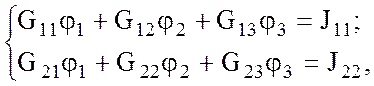
где 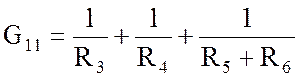 ; G11 = 1,45 См;
; G11 = 1,45 См;
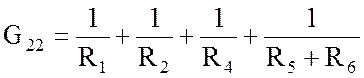 ; G22 = 0,85 См;
; G22 = 0,85 См;
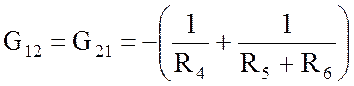 ; G12 = G21 = –0,45 См;
; G12 = G21 = –0,45 См;
![]() ;
; 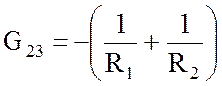 ;
; ![]() См;
См;
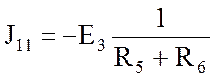 ;
; ![]() А;
А;
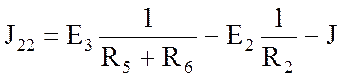 ;
; ![]() А.
А.
После подстановки имеем:
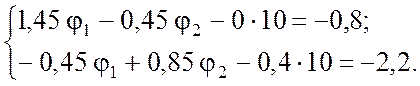
Решив систему уравнений, получим:
![]() = 0,126 В;
= 0,126 В; ![]() = 2,184 В.
= 2,184 В.
С
учетом известных потенциалов ![]() рассчитываем токи ветвей:
рассчитываем токи ветвей:
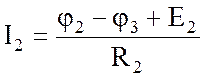 ; I2 = –0,563 А ;
; I2 = –0,563 А ;
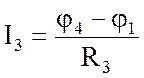 ; I3 = –0,126 А ;
; I3 = –0,126 А ;
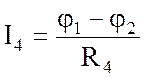 ; I4 = –0,515 А ;
; I4 = –0,515 А ;
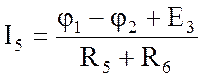 ; I5 = –0,388
А ;
; I5 = –0,388
А ;
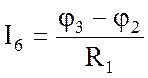 ; I6 = 1,563 А ;
; I6 = 1,563 А ;
I7 = J =2 А.
Ток I1 находим по первому закону Кирхгофа, например, для узла 3:
![]() ,
,
![]() , I1 = 2, 126 A.
, I1 = 2, 126 A.
2.7.4. Метод активного двухполюсника (эквивалентного источника)
Условие задачи. Определить ток I2 в ветви с R2 и Е2 (см. рис.2.14).
Решение.
Поскольку в ветви с R2 находится ЭДС Е2, направленная согласно с ЭДС эквивалентного источника ЕЭ, то:
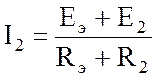
Эквивалентную ЭДС ЕЭ найдем из расчетной схемы (рис.2.15), в которой ветвь с током I2 разомкнута.
В данном случае ![]() Потенциалы
узлов 2 и 3 могут быть найдены любым из рассмотренных методов, каждый из
которых реализуется двумя уравнениями. Воспользуемся методом узловых
потенциалов.
Потенциалы
узлов 2 и 3 могут быть найдены любым из рассмотренных методов, каждый из
которых реализуется двумя уравнениями. Воспользуемся методом узловых
потенциалов.
Примем
![]() и запишем систему уравнений, в которой
и запишем систему уравнений, в которой ![]() :
:
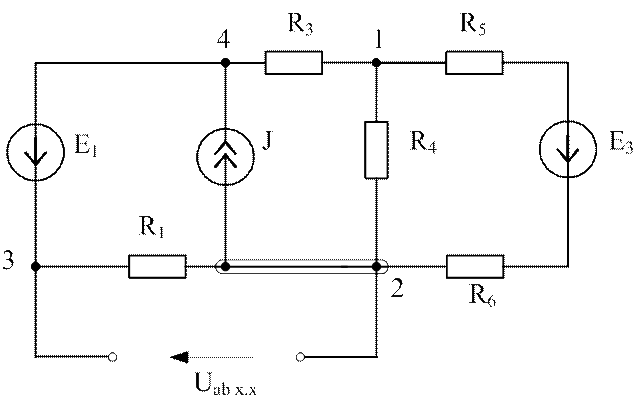
Рис. 2.15. Схема для расчета ![]()
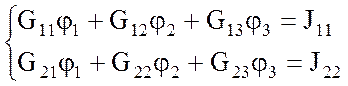
где 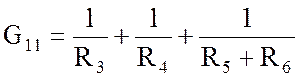 ; G11 = 1,45 См;
; G11 = 1,45 См;
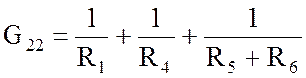 ; G22 = 0,85 См;
; G22 = 0,85 См;
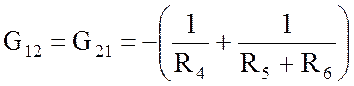 ; G12 = G21 = –0,45
См;
; G12 = G21 = –0,45
См;
![]() ;
; 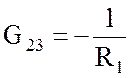 ;
; ![]() См;
См;
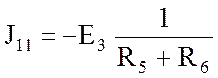 ;
; ![]() А;
А;
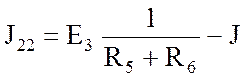 ;
; ![]() А.
А.
После подстановки и вычислений получаем:
![]()
В результате ЕЭ = 1,07 – 10 = –8,93 В.
Для определения сопротивления эквивалентного источника в схеме на рис.2.15 следует исключить все источники ЭДС, сохранив сопротивления ветвей, и разомкнуть ветвь с источником тока. Расчетная схема приобретает вид, показанный на рис.2.16.
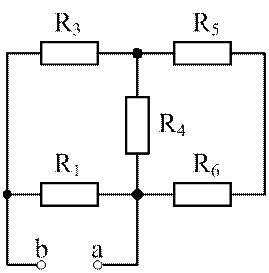
Рис 2.16. Схема для определения RЭ
Находим входное сопротивление данной схемы путем преобразования:
![]()
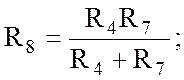
![]()
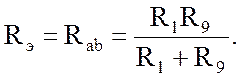
После подстановки исходных и расчетных данных получаем
![]() Ом;
Ом; 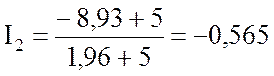 А.
А.
2.7.5. Преобразование электрических цепей
1. Замена последовательно соединенных сопротивлений одним эквивалентным (рис.2.17).

Рис. 2.17. Преобразование электрических цепей:
а – последовательное соединение сопротивлений; б – эквивалентное сопротивление
![]() .
.
2. Замена параллельно соединенных сопротивлений одним эквивалентным (рис.2.18).
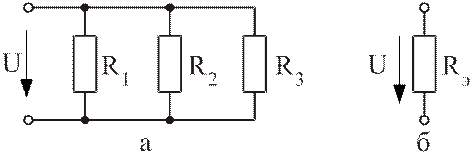
Рис. 2.18. Замена параллельного соединения сопротивлений
одним эквивалентным
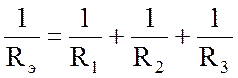 ;
;
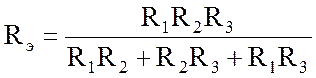 .
.
3. Замена смешанного соединения сопротивлений одним эквивалентным (рис.2.19).
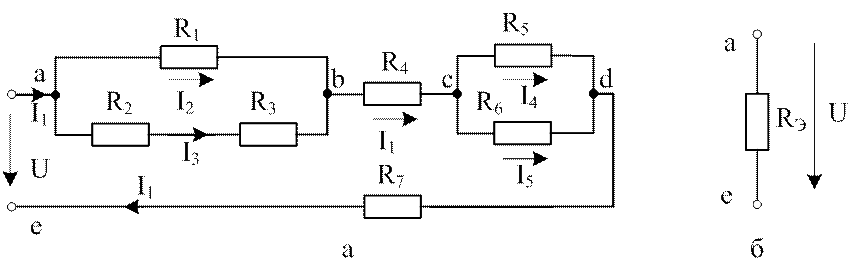
Рис.2.19. Замена смешанного соединения сопротивлений одним эквивалентным
![]()
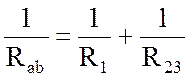 ;
;
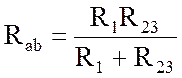 , аналогично
, аналогично 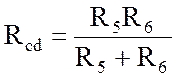 .
.
В
итоге ![]() .
.
Вводим числовые значения параметров схемы рис.2.19.
U = 48 В; R1 = 3 Ом; R2 = 2 Ом; R3 = 4 Ом;
R4 = 0,2 Ом; R5 = 6 Ом; R6 = 2 Ом; R7 = 0,3 Ом.
После подстановки:
![]() Ом;
Ом; 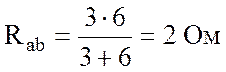 ;
; 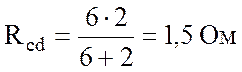 ;
;
![]()
Полученное эквивалентное сопротивление RЭ является входным (общим) сопротивлением цепи. По закону Ома входной ток
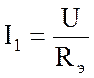 ;
; 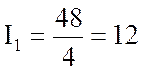 А.
А.
Токи I2 и I3 определим через напряжение Uab, токи I4 и I5 – Ucd:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.