Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 16

.                                                       (3.10)

Угол сдвига фаз в данном случае:

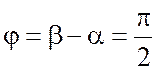.                                                 (3.11)

Соотношения (3.9) и (3.11) позволяют сделать вывод, что в индуктивности напряжение по фазе опережает ток на угол    или 90^о. Соответствующая временная и векторная диаграммы приведены на рис.3.5,а, б.

Рис.3.5. Напряжение и ток в индуктивности:

а – временная диаграмма; б – векторная диаграмма

При построении векторных диаграмм за положительное направление отсчета углов принято направление против часовой стрелки. На векторной диаграмме рис.3.5,б, соответственно, угол сдвига фаз отсчитан от вектора тока к вектору напряжения.

В качестве исходного для емкости С (см. рис.3.3,в) примем соотношение

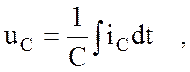                                             (3.12)

которое с учетом (3.4) приводит к уравнению

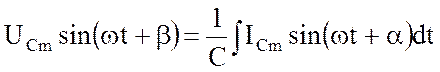
или

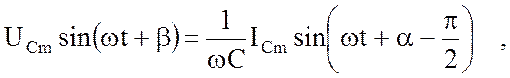
откуда получаем:

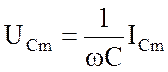;                                              (3.13)

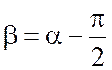;                                                (3.14)

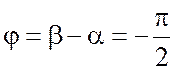.                                              (3.15)

Величина

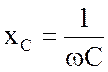     ,                                                  (3.16)

имеющая размерность сопротивления, называется емкостным сопротивлением.

В данном случае, как следует из (3.14) и (3.15), напряжение отстает от тока на угол  или на 90^о (см. рис. 3.6.а).

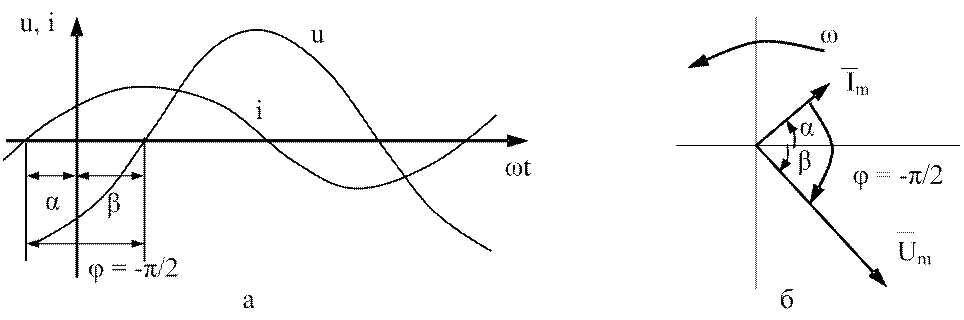
Рис.3.6. Напряжение и ток в емкости:

а – временная диаграмма; б – векторная диаграмма

Итогом рассмотрения режимов элементов  R, L и С должно быть понимание, что токи элементов и связанные с ними падения напряжения подчинены правилам:

- в сопротивлении R ток и напряжение совпадают по фазе;

- в индуктивности L напряжение опережает ток на 90⁰;

- в емкости С напряжение отстает от тока на 90⁰.

Аналогичные рассуждения могут быть проведены и для двухэлементных  схем, изображенных на рис.3.7.

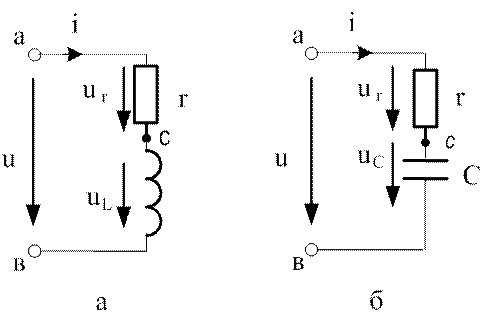
Рис.3.7. Двухэлементные схемы:

а – активно-индуктивная; б – активно-емкостная

Активно-индуктивная цепь (рис.3.7,а) описывается уравнением по второму закону Кирхгофа для мгновенных значений:

или

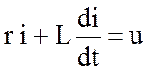.                                                  (3.17)

Как и ранее, осуществляем подстановку (3.4) в полученное уравнение:

.

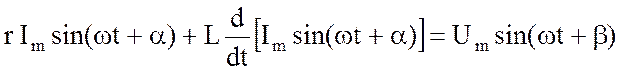Преобразуем это уравнение с использованием известных математических приемов:

;

.

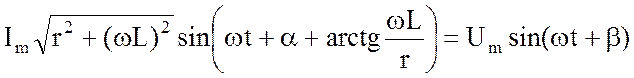На основе полученного результата формируем равенства:

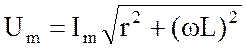      ;                                        (3.18)

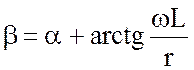   .                                                  (3.19)

Величина

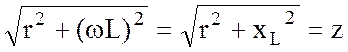                      (3.20)

называется полным сопротивлением.

Полное сопротивление содержит в своем составе активное сопротивление r. Это сопротивление отличается по величине от сопротивления, измеренного на постоянном токе в силу проявления явления поверхностного эффекта.

Суть поверхностного эффекта состоит в следующем.

Плотность переменного тока по сечению проводника распределяется неравномерно. Максимальные значения плотности тока имеют место у поверхности проводника;  минимальные – на оси проводника. Вследствие этого сопротивление проводника увеличивается по сравнению со случаем постоянного тока. Проявление поверхностного эффекта тем больше, чем больше частота тока. При пятидесяти герцах такое проявление незначительно, т.е. сопротивления, измеренные при нулевой частоте (постоянный ток) и при 50 Гц отличаются мало.

Входящее в состав полного сопротивления zиндуктивное сопротивление  х_L =  относится к разряду реактивных сопротивлений. В отличие от активного сопротивления r, которое связано с потерями электрической энергии, реактивное сопротивление x_L определяется обратимыми процессами преобразования энергии магнитного поля, которые не сопровождаются потерями электрической энергии.

В соответствии с (3.19) угол сдвига фаз в этом случае равен

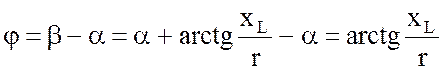  .                                  (3.21)

При конечных значениях x_L и r угол сдвига фаз может принимать любое значение между нулем и   В предельных случаях цепь становится чисто активной (L = 0) или чисто реактивной (r = 0). На рис.3.8,а изображена временная диаграмма для случая r = x_L (). Ей соответствует векторная диаграмма рис.3.8,б.