Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 9

    у         М                                                у                         у₁

                                                                                                    ·  М       

                ρ                       

                 α                                                                                                   х₁

          о        φ                   х                                 о                                х

                    х

Рис. 4.29                                                      Рис. 4.30

Введем вспомогательную систему координат R₁, получающуюся из старой переносом начала в точку О (Рис. 4.30). Пусть М(х, у)_R,  и кроме того, . По уравнениям переноса (4.8.1) и уравнениям поворота (4.8.2) имеем: , .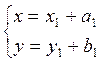

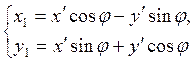Исключая из этих уравнений ненужные в окончательном результате вспомогательные координаты х₁, у₁, получаем уравнения общего преобразования координат:

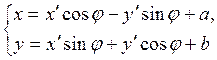                                 (4.8.3)

Пример 1. Найдите уравнения поворота координатных осей на угол 45⁰.

Решение. По формулам (4.8.2) имеем: 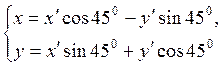 и окончательно .

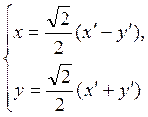Пример 2. Найдите новые координаты точки  при преобразовании координат из предыдущего примера.

Решение. Подставляем данные координаты в уравнения преобразования: 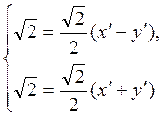. Решая эту систему, находим , то есть .

                     у                                           Пример 3. Найдите уравнение

                                                получающейся поворотом осей на угол

                     45⁰.

х                  Решение. Переходим в уравнении

                    О                                       кривой к новым координатам, пользуясь

                                                           уравнениями поворота, найденными при решении примера 1:

Рис. 4.31 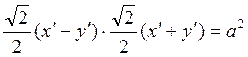                       или .

Получили уравнение равнобочной гиперболы с полуосями  (рис. 4.31)

Из решенного примера видно, что в школьном курсе, где гипербола определяется уравнением ху = , рассматривается лишь частный случай гиперболы, общее определение которой дано в § 4.3.

§ 4.9. Общее уравнение кривой второго порядка

и его упрощение путем поворота координатных осей

Мы рассмотрели важнейшие виды кривых второго порядка – эллипс, гиперболу, параболу. Теперь мы приступаем к изучению кривых, которые заданы самым общим уравнением второго порядка относительно текущих координат х и у. Наша цель – дать полную классификацию кривых второго порядка, которые называются также квадриками. Эта задача решается в §§ 4.9. – 4.12.

Самое общее уравнение второго порядка может быть приведено к такому виду:

                   (4.9.1)

Систему индексов понять легко. Считается, что букве х отвечает индекс «1», букве у – индекс «2». Индекс «12» ставится при коэффициенте члена с ху, индекс «11» - при коэффициенте члена с хх, то есть у х², и т.д. Следует только обратить внимание на то, что буквой а с индексами в трех случаях (члены с ху, х, у) обозначается не весь коэффициент, а его половина; сами же коэффициенты будут 2а₁₂, 2а₂.

Так как уравнения (4.8.3), по которым выполняется общее преобразование координат, - линейные относительно , то в результате преобразования уравнения (4.9.1) получится уравнение, которое может содержать члены второй степени (то есть члены с ), первой (с ) и свободный член. Поэтому при преобразовании координат степень уравнения может разве лишь понизиться, что было бы в случае, когда члены второй степени взаимно уничтожились. Если бы это произошло, то при обратном переходе получилось бы уравнение не второй степени, а более низкой, чего быть не может. Следовательно, при преобразованиях прямоугольных декартовых ординат уравнение второй степени переходит в уравнение второй же степени.

Полученный вывод делает определение квадрики в начале главы корректным. Он справедлив для алгебраических кривых любой степени.