Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 24

Уравнение всякой плоскости можно записать в виде (6.1.1), откуда следует, что уравнение всякой плоскости имеет первую степень относительно текущих координат х, у, z. Верно ли обратное утверждение? Положительный ответ на этот вопрос дает теорема, аналогичная теореме об общем уравнении прямой (§ 3.2).

Теорема. Всякое уравнение первой степени

                  (6.2.1)

относительно текущих координат есть уравнение плоскости, вектор  является нормальным вектором этой плоскости.

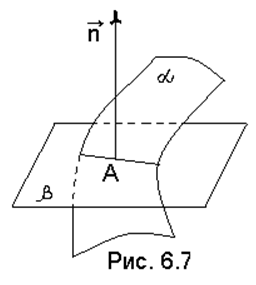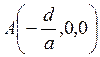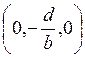          Доказательство. Обозначим буквой α поверхность, уравнение которой имеет вид (6.2.1):  (рис. 6.7) и возьмем на ней произвольную точку, например, точку . Мы считаем здесь, что , если , то по условию  и можно взять точку  или 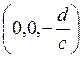. Теперь по формуле (6.1.1) найдем уравнение плоскости β по точке А и нормальному вектору : 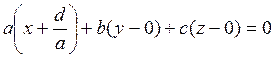, откуда после упрощений .

Таким образом, уравнения поверхности α и плоскости β совпадают. Тем самым доказано, что α – плоскость, а вектор  - ее нормальный вектор. Теорема доказана.

Следствие. Векторы  - направляющие векторы плоскости (6.2.1).

В самом деле, при .

Уравнение вида (6.2.1) называется  общим уравнением плоскости. Рассмотрим его частные случаи, которые возникают, когда некоторые коэффициенты этого уравнения обращаются в нуль. Во всех этих случаях в расположении данной плоскости α относительно координатных осей и плоскостей будут некоторые особенности.

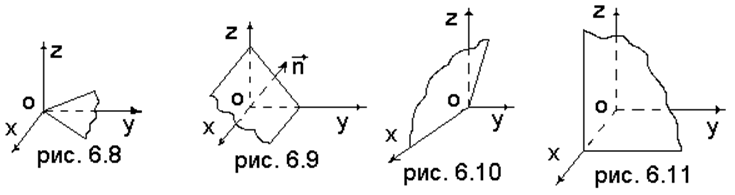
1. . В этом случае  и начало координат лежит в данной плоскости ; см. рис. 6.8.

2. В нуль обращается один из коэффициентов при переменных.

2а. . В этом случае  и нормальный вектор плоскости  параллелен плоскости YOZ или лежит в ней (рис. 6.9), а координатный вектор , перпендикулярный вектору , будет направляющим для этой плоскости. Итак, .

2в. Аналогично

3. В нуль обращаются один из коэффициентов при переменных и свободный член.

3а. . В этом случае плоскость  проходит через начало координат (так как ) и параллельна оси абсцисс (так как ). Поэтому она проходит через ось абсцисс (рис. 6.10). Итак, .

3бв. Аналогично .

4. В нуль обращаются два коэффициента при переменных.

4а. . В этом случае плоскость  параллельна оси ординат (так как ) и оси аппликат (так как ), то есть она параллельна плоскости OYZ или, что то же самое, перпендикулярна оси ОХ (рис. 6.11). Итак, .

4бв. Аналогично .

          5. В нуль обращаются два коэффициента при переменных и свободный член.

5а. . В этом случае плоскость  при  совпадает с координатной плоскостью YOZ. Итак, .

5бв. Аналогично .

Пример 1. Найдите уравнение плоскости, проходящей через ось ординат и точку А(1, 2, 2). Этот пример мы уже решали в § 6.1.

Решение. Уравнение плоскости, проходящей через ось ординат, неполное, оно имеет вид  (случай 3б). А так как точка А принадлежит этой плоскости, то . Поэтому  и мы получаем уравнение искомой плоскости: , которое после сокращения принимает вид .

Пример 2. Найдите отрезки, отсекаемые плоскостью  на координатных осях.

Решение. Точка А, в которой плоскость пересекает ось абсцисс, имеет координаты А(х, 0, 0). Подставив эти координаты в уравнение плоскости, получаем . Итак, А(2, 0, 0).

Аналогично находим точку пересечения с осями ОУ и OZ: В(0, -4, 0), С(0, 0, 4). Итак, данная плоскость отсекает на координатных осях отрезки 2, -4, 4 (рис. 6.12).

§ 6.3. Углы между плоскостями, параллельность и перпендикулярность.

Взаимное расположение двух плоскостей

Задача. Найти величину двугранного угла между плоскостями

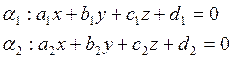                                        (6.3.1)

Решение. Эта задача аналогична задаче нахождения угла между двумя прямыми, подробно разобранной в § 3.3. Поэтому здесь изложение будет более сжатым.

Плоскости образуют два двугранных угла – φ₁ и φ₂, сумма которых равна π. Угол между нормальными векторами  и  данных плоскостей равен одному из них, на рис. 6.13 этот угол обозначен φ₁. Так как , то формула угла между плоскостями, охватывающая оба случая, имеет следующий вид: