Свойство
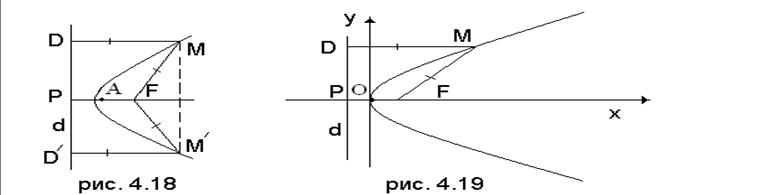
вытекает из того, что точка ![]() симметричная точке М
параболы, находится на тех же расстояниях от фокуса и директрисы, что и точка М
(рис. 4.18).
симметричная точке М
параболы, находится на тех же расстояниях от фокуса и директрисы, что и точка М
(рис. 4.18).
Определение. Ось симметрии параболы называется ее осью. Точка пересечения оси с параболой называется вершиной.
Свойство 2. Вершина параболы есть середина перпендикуляра, опущенного из фокуса на директрису.
На рис. 4.18 FP – перпендикуляр, опущенный из фокуса F на директрису d, А - его середина. Так как FA = AP, то А принадлежит параболе и, значит, является ее вершиной.
Для
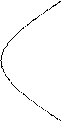
вывода канонического уравнения параболы введем систему координат: за ось
абсцисс примем ось параболы, направив ее от вершины к фокусу, за начало координат
– вершину параболы. Расстояние от фокуса до директрисы – параметр параболы
– обозначим через р, на рис. 4.19 р = FP. Тогда получим координаты
фокуса и уравнение директрисы: 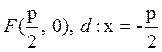 .
.
Если
М(х, у) – текущая точка параболы, то 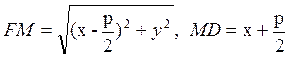 . Подставив эти выражения
в бескоординатное уравнение параболы (4.5.1), получаем уравнение параболы в
координатной форме:
. Подставив эти выражения
в бескоординатное уравнение параболы (4.5.1), получаем уравнение параболы в
координатной форме:
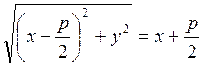 (4.5.2)
(4.5.2)
После почленного возведения этого уравнения в квадрат, раскрытия скобок и привидения подобных членов приходим к уравнению
![]() (4.5.3)
(4.5.3)
Чтобы утверждать, что получилось каноническое уравнение параболы, необходимо еще доказать, что любая точка, координаты которой удовлетворяют этому уравнению, лежит на данной параболе, то есть, что она удовлетворяет бескоординатному уравнению (4.5.1).
Пусть
координаты точки М(х0, у0) удовлетворяют уравнению
(4.5.3), т.е. ![]() ; заметим, что
; заметим, что ![]() . Тогда
. Тогда 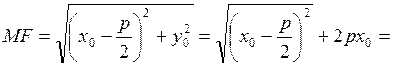
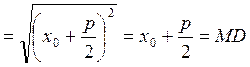 , что и требовалось доказать.
, что и требовалось доказать.
Ось параболы можно было принять не за ось абсцисс, а за ось ординат, направление координатной оси можно было тоже выбрать двумя способами. Получающиеся при этом уравнения
![]() (4.5.4)
(4.5.4)
тоже считаются каноническими. Все эти 4 случая показаны на рис. 4.20-абвг. Имея конкретное уравнение, легко понять, как расположена парабола.

![]()
![]()
![]()
![]() у у у
у
у у у
у
 |
 |
![]()
![]()
![]()
![]()
![]() о х
о х о х о х а)
о х
о х о х о х а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
Рис. 4.20
Рассмотрим, например, уравнение ![]() . Так как
. Так как ![]() и
и ![]() , то
, то ![]() , а это
значит, что парабола расположена в области отрицательных ординат (рис. 4.20-г).
, а это
значит, что парабола расположена в области отрицательных ординат (рис. 4.20-г).
Теорема (оптическое свойство параболы). Фокальный радиус произвольной точки параболы и прямая, проходящая через эту точку параллельно оси, образуют с касательной к параболе в данной точке равные углы.
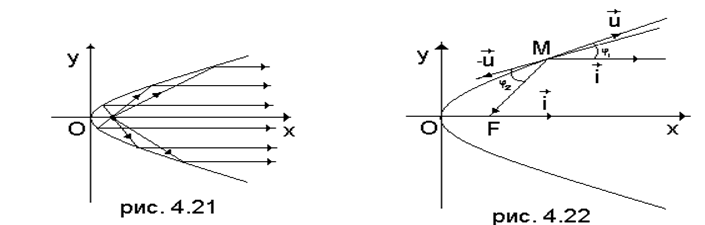
Применив закон отражения света (угол падения равен углу отражения), эту теорему можем сформулировать иначе: если из фокуса параболы выходит луч света, который отражается от параболы, то отраженный луч параллелен оси параболы (рис. 4.21). Это свойство широко используется в осветительных приборах, а также в приемной и передающей радио- и телеаппаратуре.
Доказательство осуществим прямым вычислением углов.
Пусть
дана парабола ![]() и на ней точка М(х, у); в силу
симметрии можно считать, что точка лежит в первой четверти, то есть
и на ней точка М(х, у); в силу
симметрии можно считать, что точка лежит в первой четверти, то есть ![]() (рис. 4.22). Найдем угловой коэффициент k
касательной к параболе. Для этого из уравнения
(рис. 4.22). Найдем угловой коэффициент k
касательной к параболе. Для этого из уравнения ![]() половины
параболы, расположенной выше оси абсцисс, находим производную функцию у:
половины
параболы, расположенной выше оси абсцисс, находим производную функцию у: 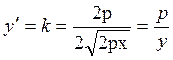 . Зная угловой коэффициент
касательной, определим, как в § 3.5, направляющий вектор касательной:
. Зная угловой коэффициент
касательной, определим, как в § 3.5, направляющий вектор касательной: ![]() .
.
 Так как М(х,
у) и
Так как М(х,
у) и 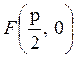 , то
, то 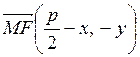 .
Направляющий вектор прямой, параллельной оси абсцисс, есть вектор
.
Направляющий вектор прямой, параллельной оси абсцисс, есть вектор ![]() . Требуется доказать равенство следующих
углов:
. Требуется доказать равенство следующих
углов: ![]() . По формуле (2.7.10) угла между векторами
. По формуле (2.7.10) угла между векторами 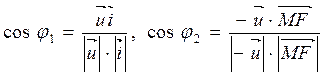 .
.
Но![]() ;
; 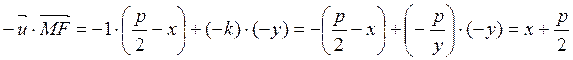 ;
;
![]() ;
; 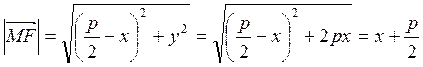 .
.
Следовательно,
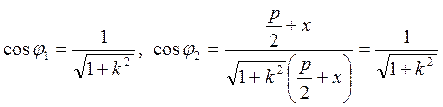 . Мы получили, что
. Мы получили, что ![]() ,
откуда следует равенство углов. Теорема доказана.
,
откуда следует равенство углов. Теорема доказана.
§ 4.6. Директрисы. Фокальное свойство эллипса и гиперболы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.