Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 28

Решение. Через прямую  проведем плоскость β перпендикулярно плоскости α (рис. 6.20). Прямая  и есть проекция прямой  на плоскость α. Уравнения прямой ₁ – это система из уравнения плоскости α (известно) и уравнения плоскости β (надо найти). Уравнение плоскости β можно найти двумя различными способами.

Первый способ. Из уранвения прямой  находим ее точку и направляющий вектор: А(1, 0, -2) и . Из уравнения плоскости α находим ее нормальный вектор: . Для искомой плоскости β оба эти вектора - направляющие. Поэтому уравнение плоскости β мы можем найти по точке и двум направляющим векторам: 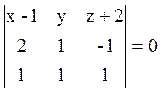 или, после упрощений, .

Второй способ. Уравнения данной прямой запишем в общем виде: 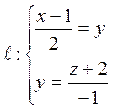 или 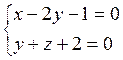. Плоскость β входит в пучок с осью , поэтому ее уравнение имеет вид  или .

В силу (6.3.4) из  следует . Отсюда  и . Получив одним или другим способом уранение плоскости β, запишем уравнения искомой прямой: .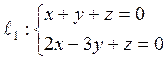

§ 6.7. Угол между прямой и плоскостью,

параллельность и перпендикулярность.

Взаимное расположение прямой и плоскости

Определение. Если прямая не перпендикулярна плокости, то углом между прямой и плоскостью называется острый угол, который эта прямая образует со своей проекцией на плоскость.

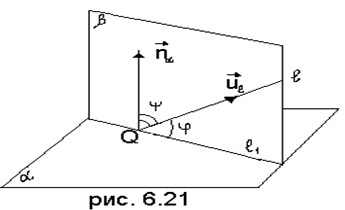          На рис. 6.21  проекция прямой  на плоскость α, β –плоскость, проходящая через  перпендикулярно α (проектирующая плоскость), , φ – угол между прямой и плоскостью. В школьном курсе доказывается, что угол φ меньше угла, который прямая  образует с любой прямой в плокости α, не паралельной и не совпадающей с ₁.

Задача. Найти угол, который прямая

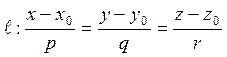 образует с плоскостью

.

Решение. Рассмотрим направляющий вектор данной прямой  и нормальный вектор данной плоскости . Для наглядности эти векторы построены из точки Q, в этом случае они распологаются в плоскости β (читателю предлагается аккуратно доказать это).

Векторы  и  могут быть направлены в одно полупространство отностельно плоскости α, как на рис. 6.21,  а могут и в разные; во втором случае векторы  и  направлены в одно полупространство. Если угол между векторами  и  острый или прямой, то обозначим его буквой , а если тупой, то  - это угол между векторами  и . Так как 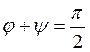, то . Поэтому 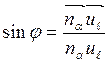 или 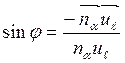. Принимая во внимание, что 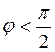 и, следовательно, , получаем 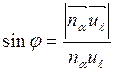. Таким образом,

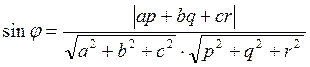                           (6.7.1)

Из этой формулы, а еще удобнее – без нее, устанавливаются условия паралельности и перпендикулярности прмой и плокости:

.

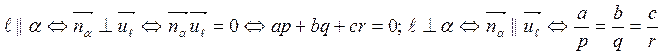Итак, мы получили условие параллельности прямой и плоскости (допускается, что прямая может лежать в плоскости)

                                               (6.7.2)

и условие перпендикулярности прямой и плокости

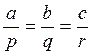                                                      (6.7.3)

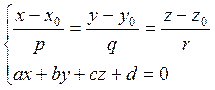Вопрос о взаимном расположении прямой и плоскости полезно также рассмотреть алгебраически. С этой целью исследуем систему, составленную из уравнений и плоскости: . В этой системе три уранения и три неизвестных х, у, z. Каждому решению системы соответствует общая точка прямой и плоскости.

Для исследования системы удобно ввести новое неизвестное t, что соответствует переходу к параметрическим уранвениям прямой. От этого число уравнений и число неизвестных увеличиваются на 1. Получается такая система: 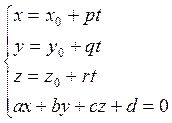. Исключая неизвестные х, у, z, получаем уравнение  или . В этом уравнении только одно неизвестное – t. Здесь могут представиться три случая.

1). Система имеет единственное решение. В этом случае прямая и плоскость пересекаются. Это будет при условии

                                               (6.7.4)

2). Система не имеет решений. В этом случае прямая и плоскость параллельны. Это будет при условии

               (6.7.5)

3). Система имеет бесконечное множество решений. В этом случае прямая лежит в плоскости. Это будет при условии

               (6.7.6)

Заметим, что условие  означает, что точка А(x₀, y₀, z₀), принадлежащая прямой , лежит также и в плоскости α. Обраим также внимание на то, что здесь вторично выведено условие параллельности (6.7.2).