§ 7.2. Эллипсоид и гиперболоиды
Определение. Эллипсоидом вращения или двуосным эллипсоидом называется поверхность вращения эллипса около одной из его осей.
Найдем уравнение эллипсоида вращения.
Пусть
в плоскости YOZ имеется эллипс 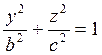 .
Согласно (7.1.1) уравнение поврехности вращения его около оси OZ
имеет вид
.
Согласно (7.1.1) уравнение поврехности вращения его около оси OZ
имеет вид 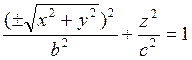 или
или
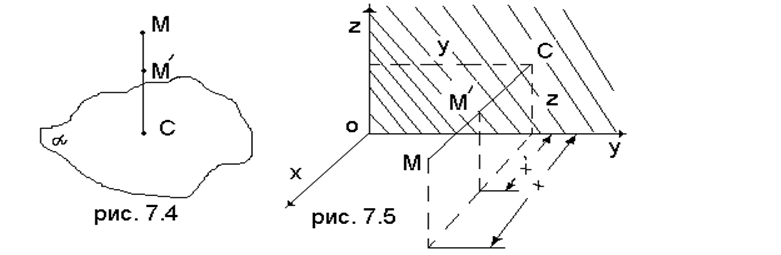
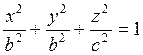 (7.2.1)
(7.2.1)
Если
теперь произвести сжатие к плоскости YOZ, то получим так называемый трехосный
эллипсоид (или просто – эллипсоид). Для того, чтобы найти его уравнение,
преобразуем уравнение (7.2.1) по формулам (7.1.2): 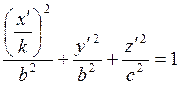 .
Обозначая
.
Обозначая ![]() и возвращаясь к обычным обозначениям
текущих координат х, у, z получаем:
и возвращаясь к обычным обозначениям
текущих координат х, у, z получаем:
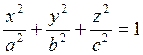 (7.2.1
а)
(7.2.1
а)
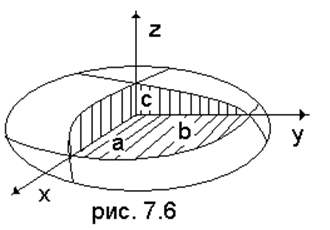
Это – уравнение трехосного эллипсоида
(рис. 7.6). Легко видеть, что на осях координат он отсекает отрезки a, b, c; эти отрезки называются
полуосями эллипсоида.
Определение. Гиперболоидом вращения называется поверхность вращения гиперболы около одной из ее осей. Если осью вращения служит мнимая ось гиперболы, то гиперболоид называется однополостным, если дейтвительная – двуполосным.
Поверхность
вращения гиперболы 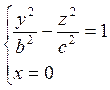 около мнимой оси OZ в
соотвествии с (7.1.1) имеет уравнение
около мнимой оси OZ в
соотвествии с (7.1.1) имеет уравнение
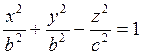 (7.2.2)
(7.2.2)
Мы получили уравнение однополостного гиперболоида вращения. После сжатия к плоскости YOZ по формулам (7.1.2) приходим к уравнению однополостного гиперболоида:
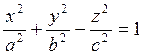 (7.2.2
а)
(7.2.2
а)
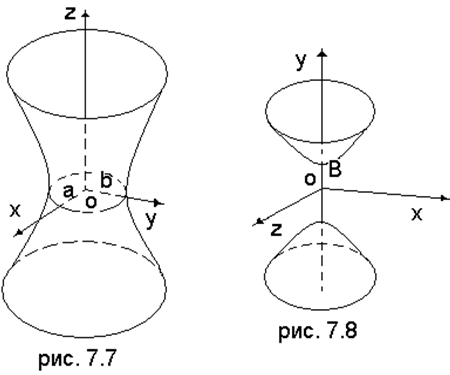
(рис. 7.7). Этот гиперболоид отсекает на осях ОХ и ОУ отрезки а и b, называемые действительными полуосями, а отрезок с на оси OZ называется мнимой полуосью.
При
вращении той же гиперболы около действительной оси ОУ получается двуполостный
гиперболоид вращения. Его ураванение получим, если в уравнение гиперболы
вместо z подставим ![]() :
:
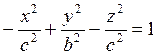 (7.2.3)
(7.2.3)
После сжатия к плоскости YOZ получаем уравнение двуполостного гиперболоида:
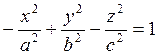 (7.2.3
а)
(7.2.3
а)
(рис.
7.8). На оси ОУ он отсекает отрезок b, называемый действительной
полуосью, а отрезки ![]() и с на осях ОХ и OZ
называеются мнимыми полуосями.
и с на осях ОХ и OZ
называеются мнимыми полуосями.
Пример.
Определить вид поверхности 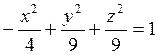 и изобразить ее на чертеже.
и изобразить ее на чертеже.
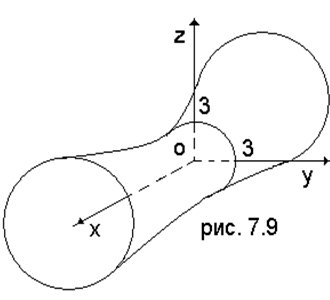
Решение. Согласно (7.2.2) это – однополостный гиперболоид вращения. Его мнимой осью, то есть осью вращения, является ось абсцисс (рис. 7.9). Из уравнения видим также, что мнимая полуось равна 2, а действительные равны 3 и 3.
§ 7.3. Параболоиды
Определние. Поверхность вращения параболы вокруг оси называется параболоидом вращения.
 Если парабола
Если парабола 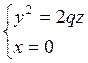 (для
определенности считаем
(для
определенности считаем ![]() ) вращается около оси OZ,
то уравнение поверхности вращения согласно (7.1.1) будет
) вращается около оси OZ,
то уравнение поверхности вращения согласно (7.1.1) будет ![]() .
.
Это – уравнение параболоида вращения, которое чаще записывают так:
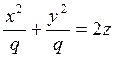 (7.3.1)
(7.3.1)
При
сжатии к плоскости YOZ получим поверхность, называемую эллипстическим
параболоидом. Его уравнение получится из уравнения (7.3.1), если его преобразовать
по формулам (7.1.2): 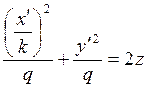 или
или
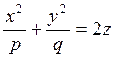 (7.3.1
а)
(7.3.1
а)
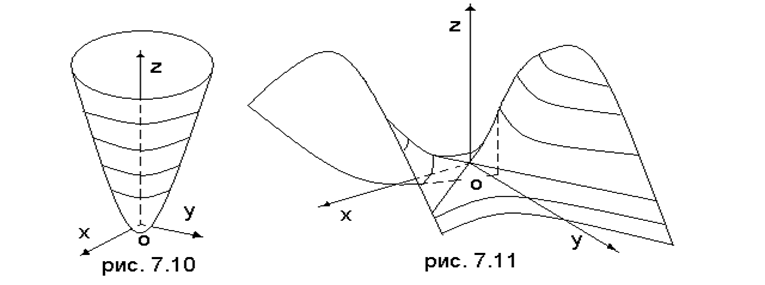
Где ![]() . Этот параболоид
показан на рис. 7.10; он называется эллиптическим потому, что его сечения
плоскостями, перпендикулярными оси OZ, то есть плоскостями
. Этот параболоид
показан на рис. 7.10; он называется эллиптическим потому, что его сечения
плоскостями, перпендикулярными оси OZ, то есть плоскостями ![]() , где
, где ![]() , суть
эллипсы
, суть
эллипсы 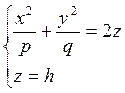 или
или 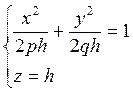 .
Убедитесь самостоятельно, что сечения эллиптического параболоида плоскостями,
параллельными XOZ и плоскостями, параллельными YOZ,
представляют собой параболы.
.
Убедитесь самостоятельно, что сечения эллиптического параболоида плоскостями,
параллельными XOZ и плоскостями, параллельными YOZ,
представляют собой параболы.
Рассмотрим теперь поверхность второго порядка
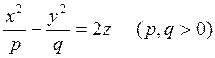 (7.3.2)
(7.3.2)
называемую гиперболическим параболоидом. Это определение формальное, оно не опирается на геометрическе свойства. Чтобы представить себе форму гиперболического параболоида, воспользуемся так называемым методом сечений. Он заключается в том, что находятся сечения поверхности семейством паралельных плоскостей, что позволяет установить, как выглядит сама поверхность.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.