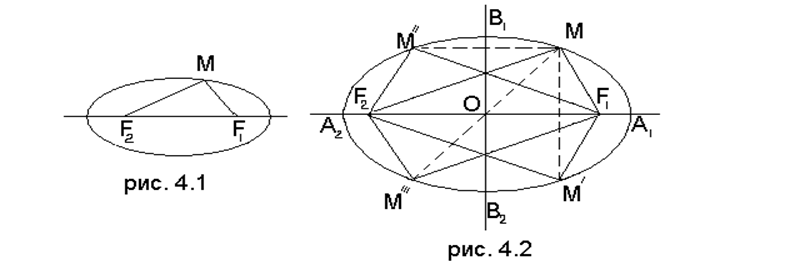
Длину отрезка F1F2 – фокусное расстояние – будем обозначать 2с, постоянную величину MF1 + MF2 (длину веревки) – 2а. Из определения эллипса ясно, что а>с; в предельном случае а=с эллипс вырождается в отрезок. Равенство
(4.1.1)
выражает характеристическое свойство эллипса, что дает нам право называть его уравнением эллипса в бескоординатной форме. Отрезки MF1 и MF2 называются фокальными радиусами точки М.
Пользуясь определением эллипса, можно установить ряд его свойств.
Свойство 1. Эллипс симметричен относительно прямой, на которой лежат фокусы.
В
самом деле, если точка 
симметрична точке М эллипса
относительно прямой F1F2 (рис.
4.2.), то 
и потому 
, а это
значит, что точка тоже лежит на эллипсе.
Свойство 2. Эллипс симметричен относительно серединного перпендикуляра отрезка, соединяющего фокусы.
Доказательство аналогично. Оно иллюстрируется тем же рис. 4.2.
Свойство 3. Эллипс симметричен относительно точки пересечения его осей симметрии. Эта точка называется центром эллипса.
В
самом деле, если точка 
симметрична точке М эллипса
относительно центра О (рис. 4.2.), то 
и
потому 
, а это значит, что лежит
на эллипсе.
Определение. Точки пересечения эллипса с осями симметрии называются вершинами эллипса. Вершины лежащие на прямой F1F2, обозначим А1 и А2 так, чтобы точки А1 и F1 лежали по одну сторону от центра эллипса, а А2 и F2 – по другую (рис. 4.2). Вершины, лежащие на второй оси симметрии, обозначим В1 и В2. Отрезок А1А2 называется большой (или фокальной) осью эллипса, а отрезок В1В2 – малой.
Свойство 4. Длина большой оси эллипса равна 2а.
Действительно,
поскольку вершина А1 лежит на эллипсе, то 
.
Но 
и 
.
Поэтому 
. А так как 
, то 
и 
, что и
требовалось доказать.
Свойство
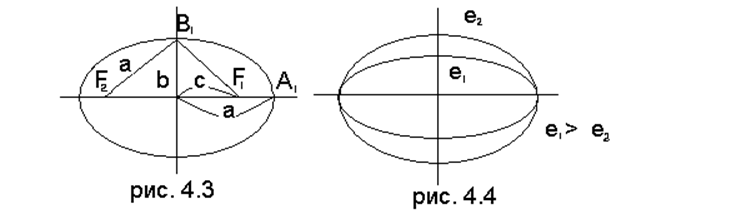
5. Большая полуось а, малая полуось bи половина с фокусного расстояния
эллипса связаны соотношением 
Вершина В1 лежит на эллипсе,
поэтому 
. А так как 
, то 
. Поэтому из треугольника 
(рис. 4.3) по теореме Пифагора сразу получаем
требуемое.
Определение. Отношение
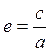называется эксцентриситетом эллипса.
Так
как 
, то 
. Если е
= 0, то и с = 0, то есть в этом случае фокусы совпадают и эллипс, как это
следует из его определения, превращается в окружность. Следовательно, окружность
есть частный случай эллипса.
Можно также рассматривать и предельный случай е = 1. В этом случае с = а и b = 0, а эллипс вырождается в отрезок F1F2 (говорят, и это точнее, - в дважды взятый отрезок).
Свойство 6. При увеличении эксцентриситета эллипс сплющивается (или, что то же самое, вытягивается).
В самом деле, если а = const, а е увеличивается, то увеличивается с и, в силу формулы (4.1.2), уменьшается малая ось 2b (рис. 4.4.).
Известно, что спутник Земли движется по эллипсу, в одном из фокусов которого находится центр земли. Спутники серии «Космос» движутся по почти круговым орбитам, эксцентриситет которых близок к нулю. Спутники связи (например, спутники серии «Молния») должны как можно дольше оставаться над территорией страны, поэтому их орбиты вытянуты, то есть имеют большие эксцентриситеты. По этому поводу смотри ниже пример 2.
Пример 1. Даны полуоси эллипса а и b. Найдите длину хорды, проходящей через фокус перпендикулярно большой оси.
Решение.
На рис. 4.5. PQ – искомая хорда, PF1 – ее половина. Если обозначить u = PF1, то по определению эллипса будет PF2 = 2a - u. Теперь по теореме Пифагора из треугольника PF1F2 получаем 
, откуда 
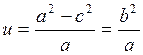и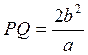 
.
Пример 2. Найдите эксцентриситет искусственного спутника Земли, если его наименьшая высота над поверхностью Земли равна р, наибольшая – q, а радиус Земли равен R (рис. 4.6). Подсчитайте эксцентриситеты двух спутников по следующим данным. Спутник Космос (запущен 13.12.63): р = 240 км, q = 613 км. Спутник Молния (запущен 14.10.65):р = 500 км., q = 25080 км. Радиус Земли равен 6370 км.
Решение.
Пусть F1 – тот
фокус эллиптической орбиты, с которым совпадает центр Земли. Легко находятся
большая ось 2а и фокусное расстояние 2с: 
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.