Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 4

Эти три свойства доказываются так же, как и для эллипса.

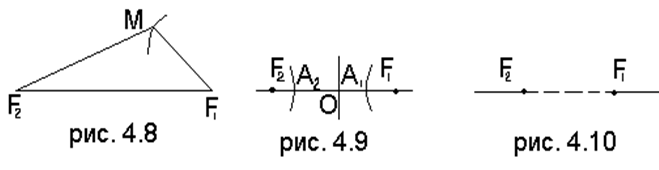
Определение. Точки пересечения гиперболы с осью симметрии, содержащей фокусы, называются вершинами гиперболы.

Вершины гиперболы А₁ и А₂ не могут быть вне отрезка F₁F₂, так как в этом случае было бы , что противоречит определению гиперболы. Они могут быть только на отрезке F₁F₂, как показано на рис. 4.9. Как и в случае эллипса, условимся нумеровать вершины так, чтобы А₁ и F₁ были по одну сторону от центра О. Отрезок А₁А₂ называется действительной (или фокальной) осью гиперболы.

Свойство 4. Длина действительной оси гиперболы равна 2а.

В самом деле, по определению , а так как , то . Но , следовательно, , откуда  и .

Свойство 5. Вторая ось симметрии не пересекает гиперболу, так как все точки этой оси равноудалены от фокусов, а точки гиперболы – нет. Поэтому гипербола состоит из двух частей (ветвей), расположенных по разные стороны от второй оси симметрии.

Определение. Отношение 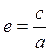 называется эксцентриситетом гиперболы.

Так как c>a, то е>1. В предельном случае е=1 будет а=с и гипербола вырождается в пару противоположно направленных лучей прямой F₁F₂ с началами в точках F₁ и F₂, причем эти лучи не имеют общих точек (рис. 4.10).

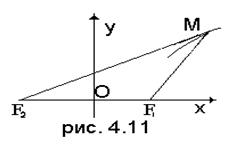
Вывод канонического уравнения гиперболы аналогичен выводу уравнения эллипса. И здесь оси симметрии принимаются за координатные (рис. 4.11)

Фокусы будут в точках F₁(c, 0) и F₂(-c, 0). Если М(х, у) – текущая точка гиперболы, то фокальные радиусы выражаются следующими формулами:

.

Подставляя эти выражения в бескоординатное уравнение гиперболы (4.3.1), получаем уравнение гиперболы в координатной форме:

                  (4.3.2)

Избавляясь в этом уравнении от радикалов точно так же, как и в случае эллипса, получаем тот же результат: , но с существенным отличием: теперь c>a. Поэтому можно ввести обозначение

                                                    (4.3.3)

Предыдущее уравнение теперь принимает следующий вид: . Разделив обе части на , получаем окончательно:

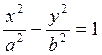                                                    (4.3.4)

Как и для эллипса, можно доказать, что последнее уравнение равносильно бескоординатному уравнения (4.3.1). Следовательно, мы получили каноническое уравнение гиперболы.

Отрезок 2b называют мнимой осью гиперболы; на чертеже ее показывают как отрезок на оси ординат с концами  и . Происхождение термина можно объяснить так. Если формально искать вторую пару вершин – точки пересечения гиперболы с осью ординат (по свойству 5 мы знаем, что таких точек не существует), - то надо решить систему уравнений 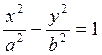, х = 0. В результате получаем «вершины» с мнимыми координатами:  и , «расстояние» между которыми, если его подсчитать по формуле (1.1.1), равно .

Если действительная и мнимая оси гиперболы равны, то есть а =в, то гипербола называется равнобочной или равносторонней. Ее каноническое уравнение таково:

                                                   (4.3.5)

§ 4.4. Изучение гиперболы по ее каноническому уравнению. Асимптоты

Изучение гиперболы мы продолжим, опираясь на ее каноническое уравнение (4.3.4).

Свойство 6. Из уравнения гиперболы следует  или . Это значит, что гипербола расположена вне полосы, ограниченной двумя перпендикулярами к действительной оси, проведенным через вершины гиперболы. На рис. 4.12 заштрихована «запрещенная» область, область, не содержащая точек гиперболы.

Это свойство усиливает доказанное в § 4.3 свойство 5.

Свойство 7. Выясним, какие из прямых, проходящих через центр гиперболы, пересекают ее. Уравнение таких прямых имеет вид . Следовательно, надо выяснить, при каких k система 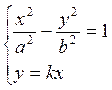 имеет действительные решения. Решаем ее методом подстановки: 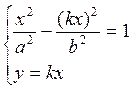.Существование решений зависит от первого уравнения, которое запишем так: 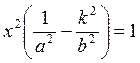. Отсюда видим, что k имеет действительные значения при условии 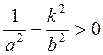, то есть при .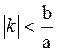

Таким образом, гипербола (4.3.4) пересекается с прямой, проходящей через центр, тогда и только тогда, когда угловой коэффициент прямой по модулю меньше .