Теорема 1. (Бескоординатный признак компланарности трех векторов). Для того, чтобы три вектора были компаланарны, необходимо и достаточно, чтобы существовала нулевая линейная комбинация этих векторов, не все коэффициенты которой равны нулю.
Иначе:
чтобы векторы ![]() были компланарны, необходимо и
достаточно, чтобы существовали числа α, β, γ, среди которых есть не равные
нулю, чтобы выполнялось равенство
были компланарны, необходимо и
достаточно, чтобы существовали числа α, β, γ, среди которых есть не равные
нулю, чтобы выполнялось равенство
![]() (5.1.2)
(5.1.2)
Доказательство.
Необходимость. Пусть векторы ![]() компланарны.
компланарны.
Если
один из них нулевой, например, ![]() , то равенство (5.1.2)
выполняется при коэффициентах 0, 0, 1:
, то равенство (5.1.2)
выполняется при коэффициентах 0, 0, 1: ![]() .
.
Если
среди данных векторов нет нулевых, но есть коллинеарная пара, например, ![]() , то по бескоординатному признаку
коллинеарности (§ 2.3) существует такое число λ, что
, то по бескоординатному признаку
коллинеарности (§ 2.3) существует такое число λ, что ![]() .
В этом случае равенство (5.1.2) выполняется при коэффициентах 0, -1, λ:
.
В этом случае равенство (5.1.2) выполняется при коэффициентах 0, -1, λ: ![]() .
.
Если
среди данных векторов нет коллинеарных, то любой из них по теореме § 2.4 о разложении
вектора на плоскости по двум неколлинеарным векторам можно представить в виде
линейной комбинации двух других, например, ![]() . В
этом случае равенство (5.1.2) выполняется при коэффициентах α, β, -1:
. В
этом случае равенство (5.1.2) выполняется при коэффициентах α, β, -1: ![]() .
.
Достаточность.
Пусть теперь выполняется равенство (5.1.2), причем среди коэффициентов есть
отличные от нуля, например, ![]() . Надо доказать, что
векторы компланарны.
. Надо доказать, что
векторы компланарны.
Из
данного равенства имеем: 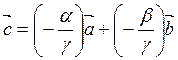 . На рис. 5.3
. На рис. 5.3 ![]() ,
, 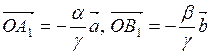 и
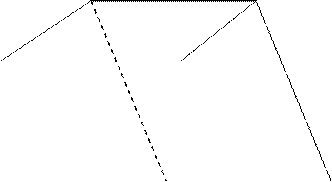
и ![]() . Из построения ясно. Что вектор
. Из построения ясно. Что вектор ![]() в плоскости (ОАВ), а это значит, что три
вектора -
в плоскости (ОАВ), а это значит, что три
вектора - ![]() - лежат в одной плоскости. Теорема доказана.
- лежат в одной плоскости. Теорема доказана.
М8 ![]()
 |
 |
||||
 |
|||||
![]()
![]()
![]()
![]()


![]() М
М
 С
С ![]() В
В

![]()
![]() А
А ![]()
![]()

![]()
![]() С
С


![]()
![]()
![]()
![]()
![]() φ
φ
![]()
![]()
![]() О
О ![]() В
М2 А1 В1
В
М2 А1 В1
![]()
![]()
![]() М1
М1
![]()
А ![]()
Рис. 5.4 Рис. 5.5
Теорема 2. (о разложении вектора на составляющие). Всякий вектор трехмерного пространства может быть единственным образом разложен по трем некомпланарным векторам.
Иначе:
надо доказать, что произвольный вектор ![]() можно
единственным способом представить в виде линейной комбинации трех данных
некомпланарных векторов
можно
единственным способом представить в виде линейной комбинации трех данных
некомпланарных векторов ![]() :
:
![]() (5.1.3)
(5.1.3)
Доказательство.
Существование. Из произвольной точки О построим векторы: ![]() ,
, ![]() (рис.
5.4). Через точку М проводим прямую параллельно ОА и точку пересечения этой
прямой с плоскостью (ОВС) обозначаем
(рис.
5.4). Через точку М проводим прямую параллельно ОА и точку пересечения этой
прямой с плоскостью (ОВС) обозначаем ![]() ; аналогично строим
точки
; аналогично строим
точки ![]() и
и ![]() .
.
Далее.
Точку пересечения плоскости (![]() ) (эта плоскость
параллельна плоскости (ОВС)) с прямой ОА обозначаем М1; аналогично
строим точки М2 и М3. Получился параллелепипед
) (эта плоскость
параллельна плоскости (ОВС)) с прямой ОА обозначаем М1; аналогично
строим точки М2 и М3. Получился параллелепипед ![]() .
.
Так
как ![]() и
и ![]() то
то ![]() .
.
В
силу бескоординатного признака коллинеарности векторов (§ 2.3) существуют
действительные числа х, у, z такие, что ![]() , и мы
приходим к разложению (5.1.3).
, и мы
приходим к разложению (5.1.3).
Единственность.
Сделаем предположение от противного, а именно, положим, что наряду с (5.1.3)
имеется разложение ![]() с другими коэффициентами
(точнее: хотя бы один коэффициент второго разложения отличен от соответствующего
коэффициента первого, например,
с другими коэффициентами
(точнее: хотя бы один коэффициент второго разложения отличен от соответствующего
коэффициента первого, например, ![]() ). Тогда
). Тогда ![]() или
или ![]() .
.
Мы
получили равную ![]() линейную комбинацию векторов
линейную комбинацию векторов ![]() с ненулевым коэффициентом z - z1. По теореме 1 это значит , что векторы
с ненулевым коэффициентом z - z1. По теореме 1 это значит , что векторы ![]() компланарны, а это противоречит условию.
компланарны, а это противоречит условию.
Полученное противоречие доказывает теорему.
Рассмотрим в трехмерном пространстве проекцию вектора на ось. Как и в плоском случае (2.6), мы ограничимся ортогональным проектированием.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.