Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 16

Через концы А и В вектора  проводим плоскости, перпендикулярные оси   (рис. 5.5). Эти плоскости пересекают ось в точках А₁ и В₁. Длина отрезка А₁В₁, взятая со знаком «+» или «-» в зависимости от направления, называется проекцией вектора  на ось .

На рис. 5.5 выполнено также дополнительное построение, которое поможет читателю понять, что и в этом случае проекция вектора на ось равна длине вектора, умноженной на косинус угла между вектором и осью:

                                                (5.1.4)

Смотри формулу (2.6.6).

§ 5.2. Координаты вектора

В § 1.2 были определены прямоугольные декартовы координаты точки на плоскости, а в § 1.7 – аффинные, являющиеся обобщением прямоугольных декартовых. Координаты вектора были введены позднее – в § 2.4. Однако проще сначала определить координаты вектора, а затем с их помощью – координаты точки, причем целесообразно делать это сразу в аффинных координатах. Определения координат вектора в настоящем параграфе и координат точки в следующем годятся для пространств любой размерности.

                                                 Аффинная система координат в пространстве

Z                                    задается точкой О и упорядоченной тройкой

                                                 векторов  (рис. 5.6).

E₃                                                           Четверка элементов , определяющая

                    E₂ Y      систему координат, называется репером,

         Е₁       O                       точка 0 – началом координат, а векторы                                                базисными или координатными. (Заметим, что в

X                                              качестве репера, задающего систему координат,

Рис. 5.6                           можно было взять также и четверку точек

(0, Е₁, Е₂, Е₃). Прямые , на которых заданы единичные отрезки , называются координатными осями (ось абсцисс  - ОХ, ординат – ОУ, аппликат – OZ). Плоскости OУZ, OXZ, ОХУ называются координатными плоскостями. Координатные плоскости делят пространство на 8 частей – октантов.

Если базисные векторы имеют равные длины и попарно перпендикулярны, то система координат называется прямоугольной декартовой, в этом случае для базисных векторов применяются стандартные обозначения .

          Определение. Координатами вектора в аффинной системе называются коэффициенты разложения данного вектора по базисным векторам.

Всякий вектор  согласно теореме 2 предыдущего параграфа можно единственным образом разложить по базисным векторам: . Числа х, у, z и есть его координаты. Напоминаем запись координат:  или .

В § 2.4 было доказано, что при сложении векторов их соответствующие координаты складываются, а при умножении вектора на число его координаты умножаются на это же число; эти свойства верны и в пространстве. Верен и координатный признак коллинеарности: чтобы два вектора  и  были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны:

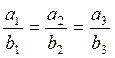                                        (5.2.1)

Теорема (координатный признак компланарности векторов). Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы определитель, составленный из их координат, был равен нулю.

Доказательство. Пусть даны векторы , , . Надо доказать, что условие их компланарности имеет вид:

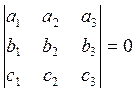                                               (5.2.2)

Необходимость. Пусть данные векторы компланарны. Тогда по бескоординатному признаку (§ 5.1) существуют числа х, у, z, среди которых есть отличные от нуля, что  или в координатной форме .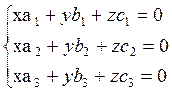

С другой стороны, эта система имеет также и нулевое решение х = у = z = 0. как известно из алгебры, система n линейных уравнений с n неизвестными имеет единственное решение в том и только в том случае, когда ее определитель не равен 0. Но мы обнаружили два различных решения нашей системы, следовательно, ее определитель равен 0, то есть выполняется условие (5.2.2).