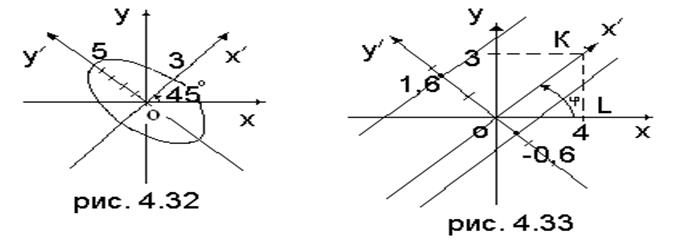
§ 4.10. Центральные квадрики и их классификация
Как показано в предыдущем параграфе, в уравнении кривой второго порядка можно поворотом координатных осей уничтожить член с произведением координат. При этом уравнение квадрики будет приведено к более простому, чем (4.9.1), виду
![]() (4.10.1)
(4.10.1)
(легко
видеть, что ![]() , но это не существенно).
, но это не существенно).
Коэффициенты
![]() и
и ![]() одновременно
равняться нулю не могут, так как при
одновременно
равняться нулю не могут, так как при ![]() уравнение (4.10.1)
было бы первой степени. Следовательно, возможны два случая: либо оба эти
коэффициента отличны от нуля. Либо один из них равен нулю.
уравнение (4.10.1)
было бы первой степени. Следовательно, возможны два случая: либо оба эти
коэффициента отличны от нуля. Либо один из них равен нулю.
Определение. Если в уравнении квадрики, в котором нет члена с произведением координат, коэффициенты при квадратах обеих переменных отличны от нуля, то квадрика называется центральной.
Название объясняется тем, что квадрика в этом случае центрально-симметрична, причем имеет только один центр симметрии; это будет установлено при помощи следующей теоремы.
Теорема. В уравнении центральной квадрики (4.10.1) переносом начала можно уничтожить члены первой степени.
Доказательство.
Перейдем от системы координат ![]() к системе
к системе ![]() по формулам (4.8.1):
по формулам (4.8.1): 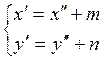 , то есть перенесем начало координат в
точку
, то есть перенесем начало координат в
точку ![]() . Уравнение квадрики в новых координатах
таково:
. Уравнение квадрики в новых координатах
таково: ![]() . После раскрытия скобок и приведения
подобных членов получаем:
. После раскрытия скобок и приведения
подобных членов получаем:
![]() , где буквой с обозначена сумма свободных
членов. Полагая
, где буквой с обозначена сумма свободных
членов. Полагая 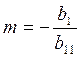 и
и 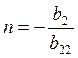 ,
получим уравнение квадрики без членов первой степени:
,
получим уравнение квадрики без членов первой степени:
![]() (4.10.2)
(4.10.2)
Теорема доказана.
Кривая
второго порядка тогда и только тогда симметрична относительно начала координат,
когда в ее уравнении отсутствуют члены первой степени, потому что только в этом
случае ее уравнение не меняется при замене х и у на –х и –у. Начало координат
поэтому есть центр симметрии кривой (4.10.2). Других центров симметрии она не
имеет, так как уничтожить члены первой степени в уравнении (4.10.2) можно, как
мы видели при доказательстве теоремы, единственным образом – переносом начала
координат в точку ![]() . Таким образом, всякая
центральная квадрика имеет единственный центр симметрии.
. Таким образом, всякая
центральная квадрика имеет единственный центр симметрии.
Примечание. Приведение уравнения (4.10.1) к виду (4.10.2) можно выполнить не только тем способом, который применен при доказательстве теоремы, но и выделением полных квадратов, как это мы делали в случае окружности в § 1.4.
Мы использовали все возможности упрощения уравнения центральных квадрики. Теперь можно дать их полную классификацию.
При
![]() центральная квадрика (4.10.2) называется невырожденной,
а при с = 0 – вырожденной.
центральная квадрика (4.10.2) называется невырожденной,
а при с = 0 – вырожденной.
Уравнение
центральной невырожденной квадрики (ЦН) легко преобразуется к каноническому
виду. Для этого достаточно в уравнении (4.10.2) перенести с вправо и разделить
уравнение на –с: 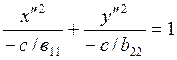 . При обозначениях
. При обозначениях 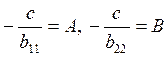 последнее уравнение принимает вид
последнее уравнение принимает вид
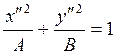 (4.10.3)
(4.10.3)
Здесь возможны три случая.
ЦН-1.
А > 0, В > 0 – эллипс с полуосями ![]() (по оси
О»х») и
(по оси
О»х») и ![]() (по оси О»у»).
(по оси О»у»).
ЦН-2. А > 0, В < 0 или А < 0, В > 0 – гипербола, действительная ось которой соответствует положительному знаменателю. А мнимая – отрицательному.
ЦН-3.
А < 0, В < 0. В этом случае уравнение (4.10.3) не удовлетворяется никакими
действительными значениями ![]() . Кривая не имеет ни
одной действительно точки. По аналогии с ЦН-1 ее называют мнимым эллипсом.
. Кривая не имеет ни
одной действительно точки. По аналогии с ЦН-1 ее называют мнимым эллипсом.
Уравнение центральной вырожденной квадрики (ЦН) получается из (4.10.2) при с = 0:
![]() (4.10.4)
(4.10.4)
Можно
считать ![]() , в противном случае уравнение умножим на
-1. Теперь могут быть две возможности.
, в противном случае уравнение умножим на
-1. Теперь могут быть две возможности.
ЦВ-1.
Если ![]() разных знаков, то есть
разных знаков, то есть ![]() и
и ![]() , то
уравнение (4.10.4) можно записать так:
, то
уравнение (4.10.4) можно записать так: ![]() или
или ![]() . Таким образом. Квадрика распадается (вырождается)
в пару пересекающихся прямых
. Таким образом. Квадрика распадается (вырождается)
в пару пересекающихся прямых ![]() и
и ![]() . Точка пересечения этих прямых – новое
начало координат
. Точка пересечения этих прямых – новое
начало координат ![]() .
.
ЦВ-
2. Если ![]() одного знака, то есть
одного знака, то есть ![]() и
и ![]() , то
уравнение (4.10.4) удовлетворяется только одной парой действительных чисел (0,
0). Левую часть уравнения в этом случае тоже можно разложить на множители, но
мнимые. Поэтому квадрику называют парой мнимых прямых, пересекающихся в
действительной точке.
, то
уравнение (4.10.4) удовлетворяется только одной парой действительных чисел (0,
0). Левую часть уравнения в этом случае тоже можно разложить на множители, но
мнимые. Поэтому квадрику называют парой мнимых прямых, пересекающихся в
действительной точке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.