Второе
уравнение не содержит ![]() . Поэтому оно представляет собой
уравнение сечения в координатной плоскости ХОУ. Рассмотрим различные случаи.
. Поэтому оно представляет собой
уравнение сечения в координатной плоскости ХОУ. Рассмотрим различные случаи.
а)
![]()
![]() В этом случае второе
уравнение системы – второй степени, поэтому в сечении получается плоская
квадрика.
В этом случае второе
уравнение системы – второй степени, поэтому в сечении получается плоская
квадрика.
б)
![]() но
но ![]() Второе
уравнение системы – первой степени, поэтому в сечении получается прямая.
Второе
уравнение системы – первой степени, поэтому в сечении получается прямая.
в)
![]() но
но ![]() Второе
уравнение системы не имеет решений, поэтому в сечении – пустое множество.
Второе
уравнение системы не имеет решений, поэтому в сечении – пустое множество.
г)
![]() В этом случае второе уравнение
удовлетворяется при любых x и y,
поэтому плоскость ХОУ представляет собой часть данной поверхности второго порядка.
Данная поверхность второго порядка имеет уравнение δ:
В этом случае второе уравнение
удовлетворяется при любых x и y,
поэтому плоскость ХОУ представляет собой часть данной поверхности второго порядка.
Данная поверхность второго порядка имеет уравнение δ: ![]() и,
следовательно, распадается на две плоскости -
и,
следовательно, распадается на две плоскости - ![]() и
и ![]()
![]()
Теорема доказана. Основной случай пересечения поверхности второго порядка с плоскостью – это случай а), когда в сечении может получится любая из 9 видов квадрик, перечисленных в § 4.12, - как действительная, так и мнимая, как невырожденная, так и вырожденная.
В качестве применения этой теоремы рассмотрим плоские сечения кругового конуса (7.4.6), не занимаясь тривиальным случаем, когда секущая плоскость проходит через вершину и в сечении получается пара прямых.
Если
плоскость пересекает все образующие конуса, то сечение ![]() располагается
с одной стороны от вершины. Оно не распадается в прямые и поэтому является
невырожденной квадрикой. Кроме того, ясно, что оно не имеет бесконечных ветвей.
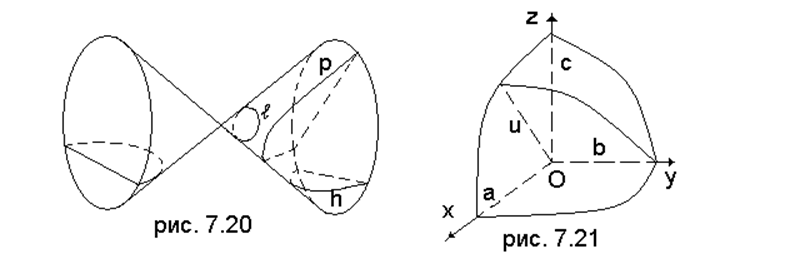
Из всех 9 видов плоских квадрик такими свойствами обладает лишь эллипс (рис.7.20).
располагается
с одной стороны от вершины. Оно не распадается в прямые и поэтому является
невырожденной квадрикой. Кроме того, ясно, что оно не имеет бесконечных ветвей.
Из всех 9 видов плоских квадрик такими свойствами обладает лишь эллипс (рис.7.20).
Если
секущая плоскость параллельна одной из образующих конуса, то сечение ![]() имеет бесконечные ветви. Оно не
распадается в прямые и состоит из одного куска. Это - парабола.
имеет бесконечные ветви. Оно не
распадается в прямые и состоит из одного куска. Это - парабола.
Если
секущая плоскость параллельна двум образующим конуса, то она пересекает обе
части конуса и сечение ![]() , следовательно, состоит из двух
кусков. Это – гипербола.
, следовательно, состоит из двух
кусков. Это – гипербола.
Таким образом, эллипс, парабола и гипербола суть конические сечения.
Теорема
2. Если плоскость ![]() пересекает
пространственную квадрику по окружности, то сечение этой квадрики плоскостью,
параллельной
пересекает
пространственную квадрику по окружности, то сечение этой квадрики плоскостью,
параллельной ![]() , есть также окружность
(когда это сечение действительно).
, есть также окружность
(когда это сечение действительно).
Доказательство.
Как и при доказательстве предыдущей теоремы, полагаем ![]() Так
как в сечении квадрики плоскостью
Так
как в сечении квадрики плоскостью ![]() получается окружность,
то
получается окружность,
то ![]() и
и ![]() (см. §
1.4).
(см. §
1.4).
Рассмотрим
сечение той же квадрики плоскостью ![]() , параллельной плоскости
, параллельной плоскости
![]() . Уравнение сечения в плоскости
. Уравнение сечения в плоскости ![]() имеет вид
имеет вид ![]()
или
с учётом найденных соотношений между коэффициентами ![]() .
.
Если это уравнение определяет действительную квадрику, то в силу того же § 1.4 оно представляет собой уравнение окружности.
Теорема доказана.
Она не решает вопроса о существовании круговых сечений, но утверждает, что если одно круговое сечение имеется, то их будет бесконечно много.
Ясно, что поверхности вращения круговые сечения имеют – это параллели. А другие квадрики ?
Теорема 3. Трёхосный эллипсоид имеет два семейства круговых сечений.
Доказательство.
Будем рассматривать эллипсоид (7.2.1а) и для определенности положим ![]() Через среднюю по величине ось проведём
плоскость (рис. 7.21). В силу теоремы 1 она пересекает эллипсоид по эллипсу. Одной
из полуосей этого эллипса будет
Через среднюю по величине ось проведём
плоскость (рис. 7.21). В силу теоремы 1 она пересекает эллипсоид по эллипсу. Одной
из полуосей этого эллипса будет ![]() ,
другую обозначим через
,
другую обозначим через ![]() . Ясно, что
. Ясно, что ![]() Если поворачивать секущую плоскость около
оси ОУ, то у эллипса, который получился в сечении, полуось
Если поворачивать секущую плоскость около
оси ОУ, то у эллипса, который получился в сечении, полуось ![]() будет меняться между
будет меняться между ![]() и
и ![]() , а
полуось
, а
полуось ![]() будет неизменна. При некотором положении
секущей плоскости получится
будет неизменна. При некотором положении
секущей плоскости получится ![]() и эллипс превратится в
окружность.
и эллипс превратится в
окружность.
Итак, мы получили круговое сечение трёхосного эллипсоида. Отсюда по теореме 2 заключаем, что он имеет семейство параллельных круговых сечений.
Второе семейство симметрично первому относительно плоскости ZОУ.
Теорема доказана. Аналогично можно было бы показать, что двумя семействами круговых сечений обладают также одно – и двуполостный гиперболоиды, эллиптический параболоид, эллиптический цилиндр, конус второго порядка. Эти два семейства сливаются в одно у поверхностей вращения. На существовании двух семейств круговых сечений основано устройство любопытных картонных моделей перечисленных поверхностей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.