Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 10

Теорема. В общем уравнении квадрики (4.9.1) путем поворота координатных осей можно уничтожить член с произведением координат.

Доказательство. В уравнении (4.9.1), в котором а₁₂ = 0, перейдем к новым координатам по формулам (4.8.2):

.

Надо показать, что за счет выбора угла поворота φ можно уничтожить член с произведением координат.

Если раскрыть все скобки и привести подобные члены, то есть члены с  и свободные, то получится уравнение того же вида, но с другими (вообще говоря) коэффициентами: .

Выпишем явно коэффициент при :

. Найдем угол φ так, чтобы этот коэффициент обратился в нуль. Для этого достаточно найти решение тригонометрического уравнения

.

Это - так называемое однородное тригонометрическое уравнение. Оно сводится к алгебраическому путем деления на cos²φ: . Получилось относительно  квадратное уравнение.

                                        (4.9.2)

заметим, что k – это угловой коэффициент новой оси абсцисс.

Дискриминант этого уравнения  положителен, поэтому уравнение имеет два различных действительных корня. Таким образом, существуют два значения tg φ, причем каждому из них соответствуют два угла в промежутке . Теорема доказана.

Из доказательства вытекает, что имеется 4 угла поворота осей координат, при которых уничтожается член с произведением.

Так как по теореме Виета два значения k удовлетворяют соотношению 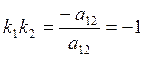, то в силу условия перпендикулярности (3.5.5) углы поворота, которые отвечают этим значениям, отличаются на . А так как углы, соответствующие одному значению k, отличаются на период тангенса π, то приходим к заключению, что четыре угла поворота, при которых уничтожается член с произведением координат, отличаются один от другого на . Для практического использования можно брать любой из них. Например, тот, который находится в первой четверти: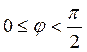

Пример 1. Путем поворота координатных осей уничтожить в уравнении кривой второго порядка  член с произведением координат.

Решение. Так как , то уравнение (4.9.2) в данном случае таково: . Решая его, получаем . Как отмечалось, достаточно взять одно значение k. Полагаем, откуда φ = 45⁰ (можно было взять и φ = 225⁰). Поэтому уравнения поворота имеют вид 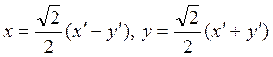 (смотри пример 1 в предыдущем параграфе). Полученные выражения подставляем в данное уравнение: 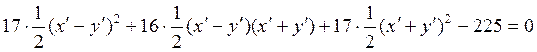. Раскрыв скобки и приведя подобные члены, получаем уравнение данной квадрики в новых координатах:  или 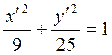. Задача решена. Данная кривая представляет собой эллипс (рис. 4.32) с полуосями, равными 3 и 5, расположенными по новым осям абсцисс и ординат соответственно.

Пример 2. Путем поворота координатных осей уничтожить в уравнении кривой второго порядка  член с произведением координат.

Решение. Так как , то уравнение (4.9.2) в данном случае таково: . Решаем его: 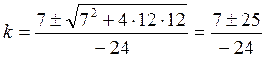 Берем положительное значение .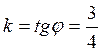

К сожалению, здесь не удастся так просто, как в предыдущем примере найти угол φ. Можно было бы найти его приближенно по таблицам или с помощью калькулятора, затем составить приближенные уравнения преобразования координат  приближенно уничтожить (то есть сделать очень малым) член с произведением координат. Но задача может быть решена и точно. Для составления уравнений поворота не нужно вычислять угол φ, а достаточно знать только sinφ и cosφ, а их можно найти из системы уравнений .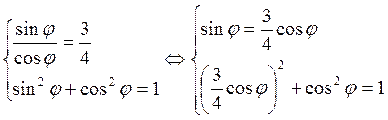

Из второго уравнения системы находим 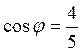 (можно было взять и ) и из первого получаем 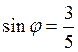. Составляем уравнения поворота (4.8.2):

.

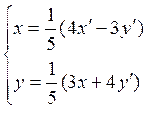Полученные выражения подставляем в уравнение данной кривой:

Раскрыв скобки и приведя подобные члены, получаем уравнение квадрики в новых координатах: .

В левой части уравнения – квадратный трехчлен относительно у. Он имеет действительные корни   и  и потому разлагается на линейные множители. Это позволяет уравнение квадрики записать в таком виде: . Следовательно, данная квадрика распадается в пару прямых  и , параллельных новой оси абсцисс.

Сделаем чертеж. Для построения новой оси абсцисс строим прямоугольный треугольник OLK (рис. 4.33), где L(4, 0), K(4, 3). Так как 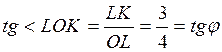, то прямая ОК – это новая ось абсцисс. Остальные построения не нуждаются в пояснениях.