Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 19

тройка векторов  - правая. При другом порядке векторов можно получить левую тройку, например, .

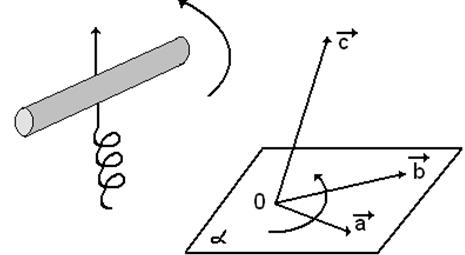          Для определения ориентации тройки векторов существуют и другие равносильные правила. Например, правило правой руки, а также способ, основанный на «наблюдении» векторов  и  из конца вектора . Ни один из таких способов не имеет никаких преимуществ перед другими. Студенту следует разобраться в каком-либо одном и научиться пользоваться им безошибочно.

Условимся тройку базисных векторов  прямоугольной системы координат брать всегда правой; в тех случаях, когда нам понадобиться левая базисная тройка, будем делать специальную оговорку.                                      

Из трех векторов можно составить 6 упорядоченных троек: ,  Применяя ко всем шести правило бураРис. 5.12                                                                                   чика, убеждаемся, что первые три имеют одну ориентацию, а последние три – другую. На этом основании мы можем сформулировать два свойства.

Свойство 1. При перестановке двухвекторов в упорядоченной тройке ориентациятройкименяется. На самом деле, при любой перестановке двух векторов в каждой из первых трех троек получится какая-либо из тех последних.Если первый вектор упорядоченной тройки  φпереставить на последнее место    (в этом случае из  получится ) или последний на первое (в этом случае из  получится ), то такая перестановка называется циклической. Непосредственно убеждаемся в справедливости следующего свойства.

Свойство 2. При циклической перестановке ориентация тройки векторов не меняется.

§ 5.5. Векторное произведение и его простейшие свойства.

Определение. Векторным произведением вектора  на вектор (обозначения:  или ) называется такой вектор, который определяется следующими условиями:

1.  Длина векторного произведения равна произведению длин перемножаемых векторов на синус угла между ними:

          (5.5.1)

2.  Векторное произведение перпендикулярно каждому из сомножителей: .

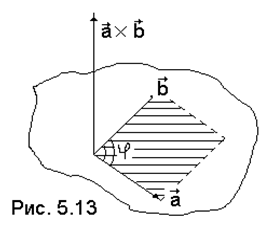
3.  Упорядоченная тройка векторов (I сомножитель, II сомножитель, векторное произведение) – правая (рис. 5.13)

Из определения вытекают простейшие свойства.

Свойство 1. Длина векторного произведения равна площади параллелограмма, построенного на перемножаемых векторах. Верно в силу формулы площади параллелограмма.

Свойство 2.  (признак коллинеарности векторов). Для коллинеарности двух векторов необходимо и достаточно, чтобы их векторное произведение равнялось 0: . Мы воспользовались формулой (5.5.1) и определением коллинеарности векторов (§ 2.1).

Свойство 3. (антикоммутативность). При перемене мест сомножителей векторное произведение меняет знак: . В соответствии с требованием 1) определения при перемене мест сомножителей длина векторного произведения не меняется, а в силу требований 2) и 3) направление меняется на противоположное.

Свойство 4. Произведения базисных векторов таковы:

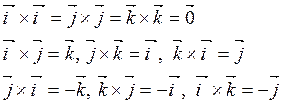                      (5.5.2)

Справедливость этих формул видна непосредственно из определения. Для запоминания формул второй и третьей строк рекомендуется схема на рис. 5.14.

Свойство 5. Числовой множитель можно выносить за знак векторного произведения:

 и                         (5.5.3)

Достаточно доказать лишь одну из этих формул, например, первую. Тогда другую можно вывести из первой на основании антикоммукативности векторного произведения. В самом деле, .

Докажем первую из формул (5.5.3).

При λ = 0 она выполняется тривиально: обе части доказываемого равенства равны.

В случае  надо доказать равенство векторов  и .

Рассмотрим два случая.

а) λ > 0 (рис. 5.15). Сначала докажем равенство длин векторов  и . Имеем по формуле (5.5.1): , . Получилось .

Теперь докажем совпадение направлений. Векторы  и  направлены по прямой, перпендикулярной плоскости векторов  и . Более того, они направлены в одну сторону, в ту, в которую направлен вектор . Действительно,  и потому тройки  и  имеют одну (правую) ориентацию, откуда следует . Но и . Поэтому . Из U = V и  вытекает , что и требовалось доказать.