Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 18

                                                                                                            C ·

                                             z

                O                У                                        У                                            У

О                                                      O

Х                                                                            х

Х                 у                                     Х

Рис. 5.7                                    Рис. 5.8                                    Рис. 5.9

Пример 2. Рассмотрим уравнение . Каждому значению пары координат (х, у) из области определения функции f соответствует значение z, то есть каждой точке плоскости ХОУ, входящей в область определения функции f, соответствует точка над ней или под ней. Таким образом, и в этом случае получается некоторая поверхность (рис. 5.8).

Пример 3. выведем уравнение сферы радиуса R с центром в точке С(, b, с).

Решение. Пусть М(х, у, z) – некоторая точка. Она лежит на сфере, если СМ = R (рис. 5.9). Но , поэтому уравнение сферы таково:

                        (5.3.4)

Линия в пространстве рассматривается как пересечение двух поверхностей и поэтому задается системой уравнений:

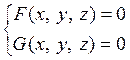                                               (5.3.5)

Пример 4. Система уравнени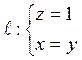й  определяет прямую. В самом деле, первое уравнение – это уравнение плоскости, параллельной плоскости ХОУ и отстоящей от нее на расстояние, равное 1; второе – уравнение плоскости, проходящей через ось OZ и делящей двугранный угол между координатными плоскостями ZOX и ZOУ пополам (рис. 5.10). Система уравнений определяет линию пересечения этих плоскостей .

Пример 5. Даны точки А(1, -1, 0) и В(3, 1, 1). Найдите уравнение множества точек, сумма квадратов расстояний от которых до двух данных точек равна 12,5.

Решение. Пусть α – искомое множество, М(х, у, z) – какая-либо точка. Тогда бескоординатное уравнение множества α согласно условию имеет вид  (рис. 5.11). По формуле (5.3.1) , . Это позволяет найти уравнение искомого множества в координатах:  или, после раскрытия скобок, привидения подобных членов и сокращения на 2 .

                    Z

                    х=у                                                                         М

                                                                                 α

                             z=1

                    O                                У

                                                                                     А        С          В

  х

Рис. 5.10                                                      Рис. 5.11

Выясним, можно ли это уравнение привести к виду (5.3.4). С этой целью, как и в § 1.4, выделяем полные квадраты:  и окончательно . Получилась сфера с центром в точке С(2; 0; 0,5), радиус которой равен 2. Легко видеть, что С – середина отрезка АВ: ее координаты равны полусуммам координат точек А и В.

§ 5.4. Ориентация некомпланарной тройки векторов

Рассматриваемое в этом параграфе понятие ориентации применимо только к некомпланарным тройкам векторов, для компланарных троек оно не имеет смысла.

Пусть  - упорядоченная тройка некомпланарных векторов и все эти векторы построены из одной точки О (рис. 5.12). Плоскость α векторов  и  делит все пространство на два подпространства. Чтобы их различать представим себе буравчик (штопор) с правым винтом, перпендикулярный плоскости α. Рукоятку будем вращать от первого вектора упорядоченной тройки ко второму по кратчайшему пути, в нашем случае – от  и ; на рисунке направление вращения показано стрелкой. При этом сам буравчик будет перемещаться перпендикулярно плоскости α в одном из двух направлений, которое и укажет нам положительное полупространство; другое полупространство – отрицательное. Смотря по тому, в какое из этих полупространств направлен третий вектор , тройка называется положительной (правой) или отрицательной (левой). На рис. 5.12