Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 22

Задача 2. Найти объем параллелепипеда и тетраэдра, построенных на векторах , , .

Решение. Объем параллелепипеда V_П находим по формулам (5.6.2) и (5.7.3):

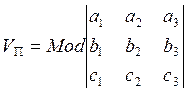                                      (5.7.7)

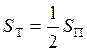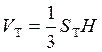Рассмотрим тетраэдр и параллелепипед, построенные на одних и тех же векторах , ,  (рис. 5.18). У них общая высота Н, а площадь основания тетраэдра S_Т в 2 раза меньше площади основания параллелепипеда S_П: . А так как объемы тетраэдра V_Т и параллелепипеда V_П выражаются формулами  и  то 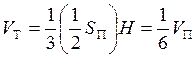. Поэтому

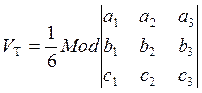                                   (5.7.8)

Пример 1. Дан тетраэдр с вершинами А(-4, 5, 3), В(-3, 2, 1), С(-2, 1, 3), D(-1, 3, 2). Найдите его высоту, опущенную из вершины А.

Решение. По формуле 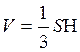, где V – объем тетраэдра, Н- его высота и S – площадь основания ВСD (рис. 5.19), имеем 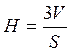. Поэтому для того, чтобы найти высоту, достаточно вычислить V и S.

Тетраэдр можно считать построенным на векторах  . По формуле (5.7.8) .

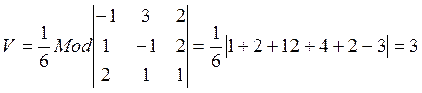Основание ВСD есть треугольник, построенный на векторах  и . Находим его площадь по формуле (5.7.5): 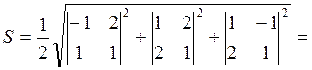 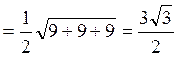. Теперь находим искомую высоту: .

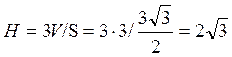Пример 2. Тройка векторов  - правая. Какую ориентацию имеет тройка ?

                                                                                                    А

 

                                                                           Н

                                                                              В                                  С

                                                                                                            D

Рис. 5.18                                            Рис. 5.19

Решение. По теореме о геометрическом смысле смешанного произведения (§ 5.6) данная задача может быть сформулирована иначе: смешанное произведение  положительно, а надо определить, какой знак имеет произведение .

Так как , то в силу дистрибутивности векторного произведения получаем:  . Далее пользуемся дистрибутивностью скалярного произведения: . Смешанное произведение, содержащее равные сомножители, равно нулю (§ 5.6, следствие 3). Кроме того, , так как циклическая перестановка не меняет смешанного произведения (§ 5.6, следствие 4). Поэтому  . Так как , то и , следовательно, тройка   - правая.

ГЛАВА 6. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ.

§ 6.1. Уравнения плоскости по точке и нормальному вектору,

по точке и двум направляющим векторам

Определение. Ненулевой вектор называется нормальным вектором плоскости, если он ей перпендикулярен.

Если  - нормальный вектор плоскости, то всякий коллинеарный ему вектор, то есть вектор , где , тоже нормальный вектор этой плоскости. Других векторов плоскость не имеет.

Точка, принадлежащая плоскости и нормальный вектор определяют плоскость. Поэтому следующая задача всегда имеет единственное решение.

Задача 1. Найти уравнение плоскости α по точке  и нормальному вектору .

Решение. Пусть  - какая-либо точка (рис. 6.1.). Тогда . А так как , то последнее условие в координатной форме имеет вид

                    (6.1.1)

 

                                                                                            

                                                                           

                                                                                                       

                                                                                                  А                 М

                                                                                              α               

          А                 М               α                                                                            

                            α

Рис. 6.1                           Рис. 6.2                                    Рис.6.3

Мы получили уравнение плоскости по точке и нормальному вектору.