Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 25

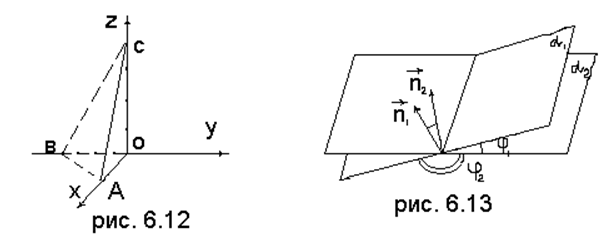
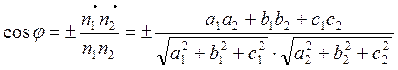                                                    (6.3.2)

Теперь выведем условия параллельности и перпендикулярности плоскостей. Имеем: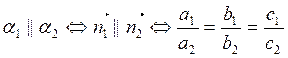  

Итак, условие параллельности (допускается и совпадение) и условие перпендикулярности двух плоскостей таковы:

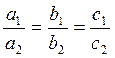                                                  (6.3.3)

                                                 (6.3.4)

Вопрос о взаимном расположении двух плоскостей удобно рассмотреть алгебраически. На этом пути мы вторично получим условие параллельности (6.3.3).

Воспользуемся теоремой Кронекера-Капелли о совместности  системы линейных уравнений. Для этого нам понадобятся основная и расширенная матрицы системы (6.3.1): 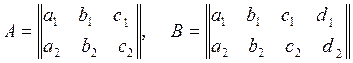, а так же их ранги, которые будем обозначать R(A) и R(B).

Так как матрица В содержит всю матрицу А и еще один столбец, то . А так как обе матрицы ненулевые и имеют по две строки, то  Поэтому для рангов возможны лишь три комбинации:

1).

2).

3).

По теореме Кронекера-Капелли в первом и третьем случаях система разрешима, так как . Но между этими двумя случаями – существенная разница. В третьем в силу условиях  все 4 пары коэффициентов обоих уравнений (6.3.1) пропорциональны и, следовательно, уравнения равносильны, а это значит, что обе плоскости совпадают. В первом же случае плоскости не совпадают, а так как они при этом имеют общие точки, то плоскости пересекаются. И, наконец, во втором случае в силу условия  система решений не имеет, а плоскости, следовательно, не имеют общих точек, то есть параллельны.

Если второй  и третий случаи – параллельность и совпадение плоскостей – объединить, то их можно отличить от первого условием , которое равносильно (6.3.3).

Вывод: для того, чтобы две плоскости были параллельными или совпадающими, необходимо и достаточно, чтобы коэффициенты при переменных в уравнениях плоскостей были пропорциональны; условием совпадения плоскостей является пропорциональность всех коэффициентов:

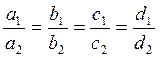                                          (6.3.5)

чтобы плоскости пересекались, необходимо и достаточно, чтобы имело место отрицание условия (6.3.3):

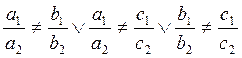                             (6.3.6)

Пример 1. Через точку А(-3, 2, 1) проведена плоскость, параллельная плоскости . Найдите ее уравнение.

Решение. Первый способ. В силу параллельности плоскостей нормальный вектор данной плоскости α есть в то же время нормальный вектор плоскости . Поэтому уравнение плоскости β можно найти по точке А и нормальному вектору (формула (6.1.1)):  или .

Второй способ. В силу условия параллельности плоскостей (6.3.3) уравнение искомой плоскости имеет вид . Неизвестный коэффициент d можно определить из условия , откуда d = 4, и мы получаем .

Пример 2. Через точки А(3, 2, -2) и В(0, 1, 1) проведена плоскость перпендикулярно плоскости . Найдите ее уравнение.

Этот пример уже решен двумя способами в § 6.1. Здесь приводится решение, в котором используется условие перпендикулярности плоскостей.

Решение. Если уравнение искомой плоскости β записать в общем виде , то из условия получаются три уравнения относительно неизвестных коэффициентов .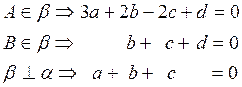

В полученной системе линейных однородных уравнений число неизвестных на 1 больше числа уравнений. В этом случае все неизвестные выражаются через одно из них.

Из второго и третьего уравнения . Исключаем 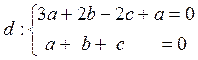, или 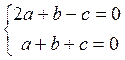. Вычитая почленно из второго уравнения первое, получаем  или . Далее находим: . Итак, уравнение искомой плоскости имеет вид  или .

§ 6.4. Расстояние от точки до плоскости

Задача. Найти расстояние от точки  до плоскости .

Решение. Расстояние h от точки А до плоскости - это длина перпендикуляра AD, опущенного из точки на плоскость: h = AD. Нормальный вектор  данной плоскости тоже перпендикулярен ей, поэтому . Следовательно, угол φ между этими векторами равен либо 0 (при  сонаправленности векторов), либо π (при противоположной направленности); на рис. 6.14 показан второй случай.