Тот факт, что при сжатии конуса вращения получается коническая поверхность вытекает из установленного нами в § 7.1 свойства, гласящего, что при сжатии прямая переходит в прямую и, следовательно, конус – в конус.
§ 7.5. Прямолинейные образующие поверхности второго порядка
Определение. Прямая, все точки которой лежат на некоторой поверхности, называется прямолинейной образующей этой поверхности.
Прямолинейными образующими обладают цилиндры и конусы второго порядка и вообще - любые цилиндры и конусы. Следующие две теоремы устанавливают значительно более интересные факты.
Теорема 1. Через каждую точку однополостного гиперболоида проходят две прямолинейные образующие.
Доказательство.
Рассмотрим сначала однополостный гиперболоид вращения (7.2.2). При пересечении
его с плоскостью ![]() получается кривая
получается кривая
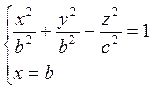 , или
, или ![]()
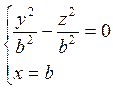 . Это кривая распадается в пару прямых
. Это кривая распадается в пару прямых 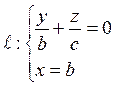 и
и ![]()
![]()
![]() :
: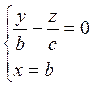
![]() проходящий через точку
А (
проходящий через точку
А (![]() ) (рис.7.19).
) (рис.7.19).
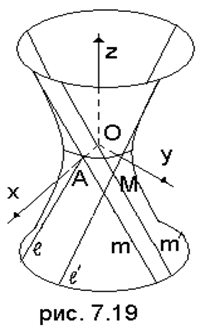
Каждая из этих прямых пересекает все
параллели и поэтому может Иначе говоря, наш гиперболоид есть поверхность вращения
прямой ![]() рассматриваться как образующая поверхности
вращения (cм. § 7.1). (или
рассматриваться как образующая поверхности
вращения (cм. § 7.1). (или ![]() ) около
оси ОZ. Поэтому через каждую точку М гиперболоида проходят
две его прямолинейные образующие: прямая.
) около
оси ОZ. Поэтому через каждую точку М гиперболоида проходят
две его прямолинейные образующие: прямая. ![]() ,
получающаяся из
,
получающаяся из ![]() путём поворота её около ОZ , и
прямая
путём поворота её около ОZ , и
прямая ![]() , аналогично получающаяся из
, аналогично получающаяся из ![]() . Прямые
. Прямые ![]() и
и ![]() - прямолинейные образующие гиперболоида.
- прямолинейные образующие гиперболоида.
Таким образом, теорема верна для гиперболоида вращения. Однополостный гиперболоид общего вида (7.2.2 а) получается из гиперболоида вращения путём сжатия. Поскольку при сжатии, как это было показано в § 7.1, прямая переходит в прямую, то теорема верна и для произвольного однополостного гиперболоида. Она устанавливает существование у него двух семейств прямолинейных образующих.
Следствие. Поверхность вращения одной из двух скрещивающихся прямых около другой есть однополостный гиперболоид вращения.
Теорема 2. Через каждую точку гиперболического параболоида проходят две его прямолинейные образующие.
Мы уже видели в § 7.3, что через начало координат проходят две прямолинейные образующие гиперболического параболоида (7.3.2). Нам предстоит существенно усилить этот результат.
Доказательство.
Уравнение (7.3.2) представим в виде 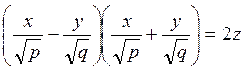 и рассмотрим две
системы:
и рассмотрим две
системы: 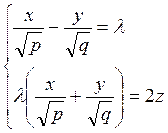
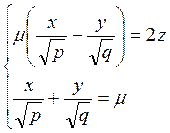 где
где
![]() и
и ![]() -
любые действительные числа.
-
любые действительные числа.
Каждая
из этих систем определяет множество (семейство) прямых, так как при любых ![]() и
и ![]() уравнения
систем – первой степени. Все эти прямые лежат на параболоиде (7.3.2), так как
уравнение (7.3.2) есть алгебраическое следствие каждой из систем: оно
получается почленным перемножением уравнений системы. Поэтому мы получили два
семейства прямолинейных образующих параболоида.
уравнения
систем – первой степени. Все эти прямые лежат на параболоиде (7.3.2), так как
уравнение (7.3.2) есть алгебраическое следствие каждой из систем: оно
получается почленным перемножением уравнений системы. Поэтому мы получили два
семейства прямолинейных образующих параболоида.
Через
произвольную точку А (![]()
![]()
![]() ) гиперболического параболоида проходит
образующая каждого семейства. Уравнения этих образующих получим, положив
) гиперболического параболоида проходит
образующая каждого семейства. Уравнения этих образующих получим, положив 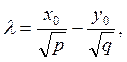
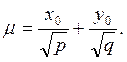 В
том, что при этих значениях
В
том, что при этих значениях ![]() и
и ![]() образующие проходят через точку А, легко
убедиться непосредственно.
образующие проходят через точку А, легко
убедиться непосредственно.
Примечание
.Теорему 1 настоящего параграфа можно было доказать аналогично, представив
уравнение однополостного гиперболоида (7.2.2 а) в виде 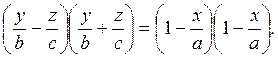 Читателю
предлагается такое доказательство выполнить самому.
Читателю
предлагается такое доказательство выполнить самому.
На теоремах этого параграфа основано устройство нитяных моделей однополостного гиперболоида и гиперболического параболоида.
§ 7.6. Плоские сечения пространственных квадрик.
Плоские квадрики как конические сечения
Теорема 1. Всякое сечение поверхности второго порядка плоскостью есть либо плоская квадрика, либо – прямая, либо пустое множество, либо же секущая плоскость включается в данную поверхность.
Доказательство.
Пусть имеется пространственная квадрика ![]() и
плоскость
и
плоскость![]() . Выберем прямоугольную декартову систему
координат, приняв плоскость
. Выберем прямоугольную декартову систему
координат, приняв плоскость ![]() за координатную
плоскость ХОУ, а в остальном – произвольно. В этих координатах
за координатную
плоскость ХОУ, а в остальном – произвольно. В этих координатах
![]() : z = 0,
: z = 0,
![]() :
: ![]()
![]() .
.
Сечение определяется системой этих двух уравнений. Подставив во второе уравнение z = 0, получаем равносильную систему
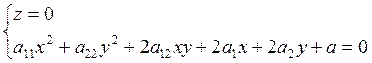 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.