Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 3

Теперь находим эксцентриситет: :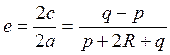

Для спутника Космос:.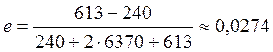

Для спутника Молния: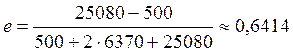

.

§ 4.2. Каноническое уравнение эллипса

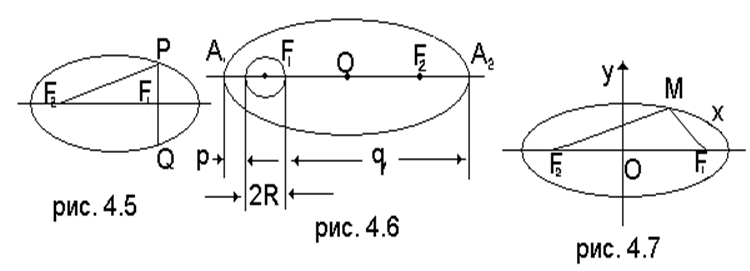
Прямую F₂F₁ примем за ось абсцисс, центр О эллипса – за начало координат, луч OF₁ – за положительный луч оси абсцисс (рис. 4.7). Выведем уравнение эллипса в этой системе координат.

Так как , то . Пусть М(х, у) – текущая точка эллипса. По формуле расстояния между двумя точками находим ее фокальные радиусы: .

Подставляя эти выражения в бескоординатное уравнение эллипса (4.1.1), получаем уравнение эллипса в координатной форме:

                  (4.2.1)

Это уравнение можно упростить, избавившись от радикалов. Для сокращения выкладок введем обозначение , которое придает уравнению эллипса следующий вид:. Обе части уравнения возводим в квадрат: . После очевидных упрощений получаем: .

Еще раз возводим уравнение почленно в квадрат: , откуда . Возвращаемся к прежним обозначениям:  или . На основании формулы (4.1.2) это можно записать еще короче: . Наконец, разделив обе части уравнения на , получаем каноническое уравнение эллипса:

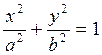                                                    (4.2.2)

Впрочем, в настоящий момент у нас еще не может быть уверенности в том, что полученное уравнение есть уравнение эллипса, так как при преобразованиях уравнения (4.2.1) мы пользовались почленным возвышением уравнения в квадрат, что может породить посторонние  решения; например, уравнения х=у и х²=у² не равносильны: первое – уравнение прямой, второе – уравнение пары прямых. Поэтому следует еще доказать, что любая точка, координаты которой удовлетворяют уравнению (4.2.2), лежит на данном эллипсе, то есть, что она удовлетворяет бескоординатному уравнению (4.1.1).

Итак, пусть координаты точки М(х₀, у₀) удовлетворяют уравнению (4.2.2), то есть 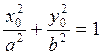 или 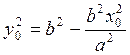. Надо показать, что выполняется условие (4.1.1). Имеем:

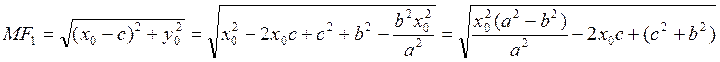. Два раза применяем формулу (4.1.2): .

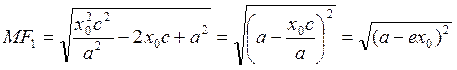Отсюда . Аналогично .

Так как точка М удовлетворяет уравнению (4.2.2), то , кроме того е<1. Перемножая почленно эти неравенства, получаем , поэтому . Следовательно,

                            (4.2.3)

Таким образом, .

Это значит, что условие (4.1.1) удовлетворено, и потому (4.2.2) - действительно уравнение эллипса.

Пример 1. Найдите каноническое уравнение эллипса, если его большая ось равна 12, а эксцентриситет равен .

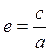Решение. Дано: а=12, . Так как , то 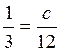, откуда с=4. Теперь по формуле (4.1.2) . Поэтому каноническое уравнение данного эллипса таково: .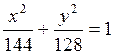

Пример 2. Даны полуоси эллипса  и b. Найдите длину хорды, проходящей через фокус перпендикулярно большой оси.

Эта задача уже решалась в § 4.1. Здесь для ее решения воспользуемся каноническим уравнением эллипса.

Решение. Мы будем пользоваться рис. 4.5, хотя на нем не указаны координатные оси. Один из концов искомой хорды PQ, точка Р, имеет координаты Р(с, у). Так как эта точка лежит на эллипсе, то 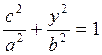, отсюда . Следовательно,  и .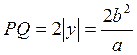

§ 4.3. Гипербола. Ее простейшие свойства и каноническое уравнение

Определение. Гиперболой называется множество точек, модуль разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.

Фокусы обозначаем F₁ и F₂ , текущую точку гиперболы – М (рис. 4.8). Если участвующую в определении постоянную величину обозначить 2а, то бескоординатное уравнение гиперболы принимает вид

                                             (4.3.1)

Из треугольника MF₁F₂ получаем . Обозначая, как и в случае эллипса, , имеем ; напоминаем, что в случае эллипса мы имели неравенство противоположного смысла.

Рассмотрим свойства гиперболы, вытекающие непосредственно из определения.

Свойство 1. Гипербола симметрична относительно прямой, на которой лежат фокусы.

Свойство 2. Гипербола симметрична относительно серединного перпендикуляра отрезка, соединяющего фокусы.

          Свойство 3. Гипербола симметрична относительно точки пересечения ее осей симметрии. Эта точка называется центром гиперболы.