Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 8

                                       эллипс

                           F

р                                                                                                ρ

                                                                                                     φ

P                   

                                                                                     P      F                       L

Рис. 4.25                                                      Рис. 4.26

Это уравнение обычно записывают в виде, разрешенном относительно 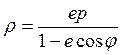. Обозначив , получаем окончательно

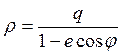                                                 (4.7.1)

В случае эллипса  знаменатель всегда положителен, поэтому ρ при всех значениях φ имеет положительные значения. В случае параболы   знаменатель обращается в нуль при φ = 0 – на параболе нет точки, для которой φ = 0; в остальных случаях . В случае гиперболы  дело обстоит несколько сложнее. При  знаменатель в уравнении (4.7.1) обращается в нуль и ρ не существует. В § 4.4, рассматривая свойство 9, мы видели, что при условии  угол φ равен половине угла между асимптотами; там для этой половины было обозначение α. На гиперболе нет точек, для которых φ=α или φ=α.

При , то есть при 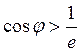 будет , и придется пользоваться обобщенными полярными координатами (§ 1.8), то есть надо полярный  радиус откладывать в противоположном направлении или, что то же самое, полярный угол изменять на π: вместо φ в этом случае берется φ + π.

Легко установить, что при  получается вторая ветвь гиперболы, а при  - первая.

§ 4.8. Преобразование координат

Вопросы, которые будут рассмотрены в этом параграфе, строго говоря, в тему «Квадрики» не входят. Однако выделять их в отдельную главу нет смысла, а для дальнейшего изучения квадрик они нужны.

Нам предстоит решить следующую задачу. Пусть имеются две системы прямоугольных декартовых координат – R (старая) и  (новая). Произвольная точка М в старой системе имеет координаты х, у, а в новой - ; это записывается так М(х, у)_R и . Необходимо найти уравнения перехода от системы R к системе , то есть х и у надо выразить через  (или наоборот).

      у         М(х, у)_R

               ·                                                              y                           

                                                                                                М

           

                                                     y                                                                  

                                                                    b  

                       Φ                                                                                          х

   O                                  x                           О          а             

         

Рис. 4.27                                  Рис. 4.28                   х

Это – пока неполная постановка задачи. Еще необходимо, чтобы новая система была как-то задана относительно старой. Например, можно задать координаты нового начала в старой системе   и угол φ между старой и новой осями абсцисс (рис. 4.27).

Рассмотрим сначала частные случаи преобразования координат.

1.  Перенос начала. Это преобразование заключается в том, что координатные оси перемещаются параллельно, а базисные векторы  и  не меняются (рис. 4.28).

Если М(х, у)_R,  и , то

.

Но , поэтому

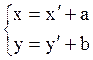                                                      (4.8.1)

Это и есть уравнение переноса начала координат.

2.  Поворот осей. Преобразование заключается в том, что координатные оси поворачиваются на некоторый угол φ около начала (рис. 4.29).

Обозначим, как обычно, М(х, у)_R,  и, кроме того, . Тогда  и . Так как вектор  образует с осями ОХ и  углы α + φ и α соответственно, то по формулам (2.6.7) получаем: 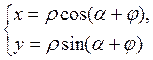,  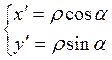   . Поэтому

.

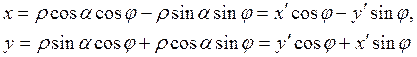Итак, уравнения поворота осей имеют вид

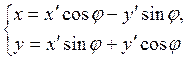                                      (4.8.2)

3.  Общий случай. Начало смещено в точку  и оси повернуты на угол φ.