Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 5

В пучке прямых, проходящих через начало координат, прямые с угловыми коэффициентами 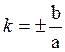, разделяют прямые пучка на те, которые пересекают гиперболу, и те, которые ее не пересекают; сами же эти прямые гиперболу не пересекают.

Определение. Прямые 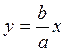 и 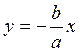 называются асимптотами гиперболы.

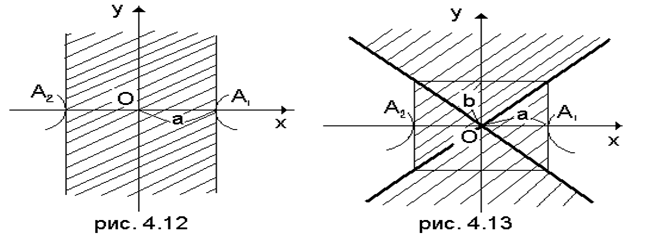
Из свойства 7 вытекает, что гипербола располагается внутри пары вертикальных углов, образованных асимптотами; имеются в виду та пара углов, в которых находится действительная ось гиперболы. Асимптоты легко построить на чертеже. Для этого надо сперва построить прямоугольник, для которого оси гиперболы 2а и 2b служат средними линиями (рис. 4.13). Прямые, содержащие диагонали этого прямоугольника, суть асимптоты, так как их угловые коэффициенты, как и угловые коэффициенты асимптот, равны  и .

На рис. 4.13 заштрихована область, в которой нет точек гиперболы. Как видим, по сравнению с рис. 4.12 «запрещенная» область увеличилась.

Свойство 8. (основное свойство асимптот). При удавлении точки гиперболы от вершины в бесконечность её расстояние до одной из асимптот стремится к нулю.

Для доказательства в силу симметрии гиперболы достаточно рассмотреть ту часть гиперболы, которая находится в первой четверти. Возьмем точку гиперболы М(х, у), где х>0, у>0. На рис. 4.14 MD – расстояние от точки М до асимптоты 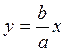. Требуется доказать, что .

Через точку М проведем прямую параллельную оси ординат и обозначим ее точки пересечения с осью абсцисс и асимптотой через N и К соответственно. Тогда .

Длина отрезка NK – это ордината той точки асимптоты, которая имеет абсциссу х; эту ординату находим из уравнения асимптоты: 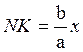. Аналогично находим длину отрезка NM как ординату той точки гиперболы, которая имеет абсциссу, равную х: .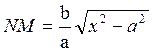

Поэтому 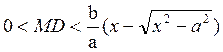. Но 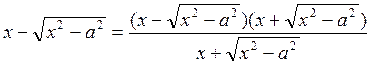 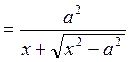, откуда  и следовательно, , что и требовалось доказать.

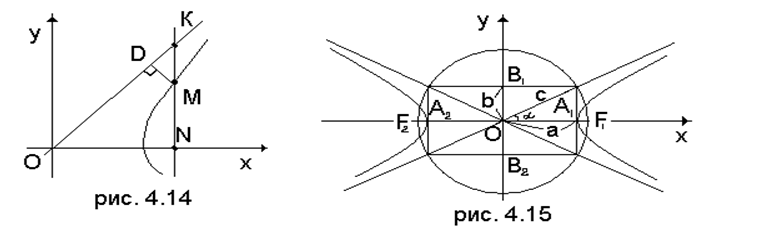
Исходя из доказанных свойств, можно представить себе форму гиперболы, см. рис. 4.15. Там же на основании соотношения (4.3.3) построены фокусы гиперболы.

Свойство 9. Выясним, как эксцентриситет гиперболы влияет на ее форму.

Как отмечалось, гипербола находится внутри пары вертикальных углов, образованных асимптотами. Величину каждого из этих углов обозначим 2d (рис. 4.15). Так как 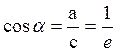, то чем больше эксцентриситет гиперболы, тем больше угол между ее асимптотами. Если же , то . В предельном случае  будет  и гипербола «сплющиться» в пару дважды взятых лучей; этот предельный случай уже встречался, см. § 4.3. и рис. 4.10.

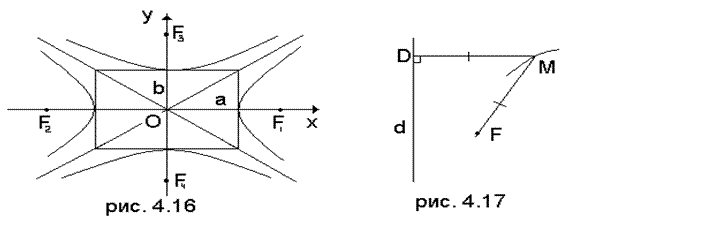
          Определение. Если действительная ось одной гиперболы служит мнимой осью другой и наоборот, то такие гиперболы называются сопряженными. (рис. 4.16).

Из определения ясно, что у сопряженных гипербол общие асимптоты. В силу соотношения (4.3.3) у них равны фокусные расстояния.

Уравнения сопряженных гипербол: 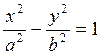 и .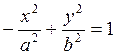

Обратите внимание: в этих уравнениях знак «+» соответствует действительной оси, знак «-» - мнимой.

Пример. Найдите каноническое уравнение гиперболы, если фокусное расстояние равно 8. а угол между асимптотами равен 120⁰.

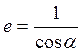Решение. Пользуясь принятыми обозначениями, запишем данные: . Так как , то 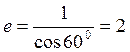. Из определения эксцентриситета 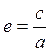 имеем 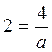,  откуда . По формуле (4.3.3) . Поэтому уравнение искомой гиперболы таково: .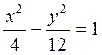

§ 4.5. Парабола. Ее свойства и каноническое уравнение

В школьном курсе дается формальное определение параболы как кривой, уравнение которой имеет вид у = ах². Здесь мы определим параболу путем указания ее характеристического свойства, не использующего понятие координат.

Определение. Параболой называется множество точек, равноудаленных от данной прямой (директрисы) и не лежащей на ней точки (фокуса).

На рис. 4.17 F – фокус, d – директриса, М – точка параболы. По определению фокальный радиус FM точки М равен расстоянию MD этой точки до директрисы:

                                  (4.5.1)

Это – бескоординатное уравнение параболы.

Рассмотрим простейшие свойства параболы.

Свойство 1. Парабола симметрична относительно прямой, проходящей через фокус перпендикулярно директрисе.