Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 13

ЦН-1	Эллипс
ЦН-2	Гипербола
ЦН-3	Мнимый эллипс
ЦВ-1	Пара пересекающихся прямых
ЦВ-2	Пара мнимых прямых. Пересекающихся в действительной точке	·
ПН	Парабола
ПВ-1	Пара параллельных прямых
ПВ-2	Пара совпавших прямых
ПВ-3	Пара мнимых параллельных прямых

Итого получилось 9 видов квадрик. В том числе:

5 центральных и 4 параболических;

4 невырожденных и 5 вырожденных, причем вырожденные во всех случаях распадаются в пару прямых;

6 действительных и 3 мнимых.

В соответствии с изложенным в § 4.9 – 4.11 привидение общего уравнения (4.9.1) к простейшему виду надо выполнять так.

1. Если в уравнении квадрики есть член с произведением координат, то поворотом координатных осей его надо уничтожить; угол поворота определяется уравнением (4.9.2). После этого определяется тип квадрики – центральная или параболическая.

2. Если квадрика центральная, то переносом начала в центр симметрии привести уравнение к простейшему виду (4.10.2), определить вид квадрики и, если она действительная, сделать чертеж.

3. Если квадрика параболическая невырожденная. То переносом начала в вершину параболы привести уравнение к простейшему виду (4.11.2) и сделать чертеж.

4. Если квадрика параболическая вырожденная, то левую часть ее уравнения (4.11.3) разложить на множители и, если квадрика действительная, сделать  чертеж.

В заключение приведем два примера с полным решением.

Пример. 1. Привести к простейшему виду уравнение кривой второго порядка . Сделать чертеж.

Решение. Так как , то начинаем с поворота осей. Из уравнения (4.9.2), где , определим угол поворота. Имеем: . берем положительный корень: . Отсюда .

Уравнения поворота на 45⁰ уже встречались (§ 4.8, пример 1):

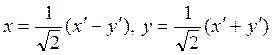. По этим формулам преобразуем данное уравнение: 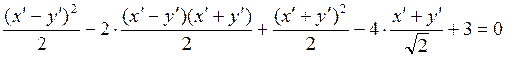. После упрощений: .

Так как , а , то полученное уравнение есть уравнение ПН квадрики – параболы. Упрощаем это уравнение дальше путем переноса начала координат по формулам (4.8.1): . Уравнение параболы в системе  имеет вид:  или . Выбираем m и n так, чтобы уничтожились члены с  и свободный. Для этого полагаем  . Отсюда .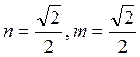

Значит, при переносе начала координат в точку 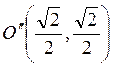 уравнение параболы приводится к каноническому виду . Параметр параболы равен 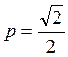. Смотри рис. 4.35.

Пример 2. Привести к простейшему виду уравнение кривой второго порядка . Сделать чертеж.

                       у                                                                    у   

                                                                                               ·  1          К

                                       45⁰     х                                                       φ    L

                        о               1                                                    ·о                       3                        х

Рис. 4.35                                                      Рис. 4.36