Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 29

Пример 1. Выяснить взаимное расчположение прямо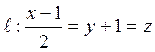й  и плоскости .

Решение. Проверяем выполнение условий (6.7.4) – (6.7.6). В данном случае . Поэтому , .

Выполняется условие (6.7.6). Следовательно,  - прямая лежит в плоскости.

Пример 2. Выяснить взаимное расположение прямо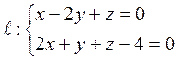й  и плоскости .

Решение. Первый способ. Находим по формуле (6.6.5). Направляющий вектор прямой  (рис. 6.22): 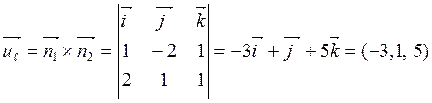. Известен и нормальный вектор плоскости . Так как , то . Следовательно, данные прямая и плоскость пересекаются.

Второй способ. Рассмотрим систему, состоящую из уравнений прямой и плоскости: 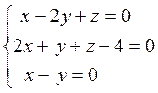. Это – система трех уравнений с тремя неизвестными. Ее определитель 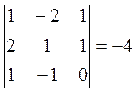 отличен от нуля. Поэтому система имеет единственное решение, а это означает, что означает, что прямая и плосксоть имеют единственную общую точку, то есть пересекаются.

§ 6.8. Угол между прямыми. Взаимное расположение двух прямых

Если две прямые пересекаются, то они образуют 4 угла, попарно равных. Поэтому имеет смысл говорить о двух углах между ними. Угол между паралельными или совпадающими прямыми считается равным 0 или π. Если прямые скрещиваются, то за углы между ними принимаются углы, образованные пересекающимися прямыми, параллельными данным скрещивающимися. На рис. 6.23 показаны углы φ₁ и φ₂ между скрещивающимися прямыми  и , эти углы образолваны прямыми  и  проходящими через точку Q параллельно  и . Для наглядности на рисунке через прямые ,  и точку Q проведены параллельные плоскости.

Из сказанного следует, что угол между произвольными прямыми

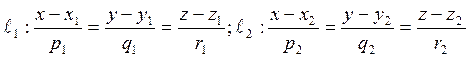          (6.8.1)

равен углу между их направляющими векторами  и  или составляет в сумме с ним π. Поэтому

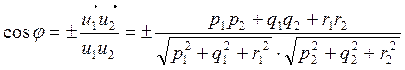                     (6.8.2)

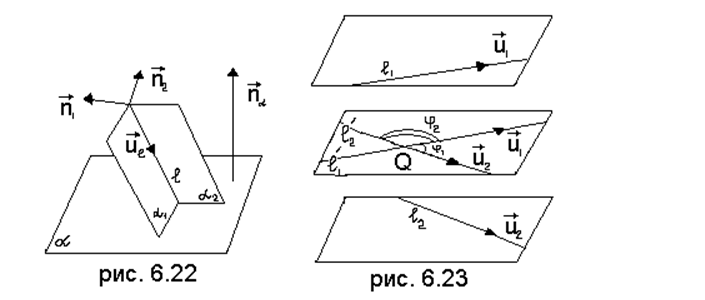
Мы получили формулу угла между двумя прямыми в пространстве.

Тривиальным образом получаем также условие паралельности

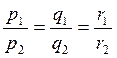                                                  (6.8.3)

и условие перпендикулярности

                             (6.8.4)

двух прямых в пространстве.

Вопрос о взаимном расположении двух прямых в пространстве затруднительно рассматривать чисто алгебраически, ибо система уравнений (6.8.1) не имеет решений как в случае параллельных прямых, так и в случае скрещивающихся.

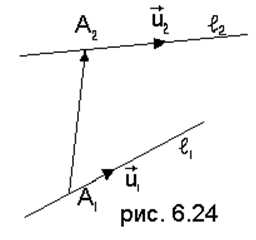                                                 На рис. 6.24 использованы прежние обозначения и, кроме того, показаны точки  и

. Если прямые  и  лежат в одной плоскости, то тройка векторов компланарна

Если эти прямые не лежат в одной плоскости, то есть скрещиваются, то эта тройка не компланарна.

Компланарность тройки векторов зависит от определителя

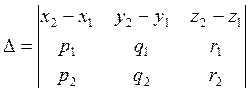                            (6.8.5)

составленного из их координат (смотри теорему  в § 5.2). Если , то прямые в одной плоскости, если  - скрещиваются.

Если , то есть в определителе (6.8.5) вторая и третья строки пропорциональны между собой, но не пропорциональны первой, то прямые параллельны.

Если , то есть все строки определителя пропорциональны, то прямые совпадают. Если вторая и третья строки не пропорциональны, но , то прямые пересекаются.

Результаты исследования сведем в таблицу.

ГЛАВА 7. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА.

В этой главе рассматриваются поверхности второго порядка (или пространственные квадрики), то есть поверхности, уравнения которых – второй степени относительно прямоугольных декартовых координат. Корректность такого определения, то есть его независимость от выбора системы прямоугольных декартовых координат, можно доказать подобно тому, как в § 4.9 была доказана корректность определения плоских квадрик.