Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 32

Рассмотрим сечения гиперболического параболоида (7.3.2) плоскостями , где . Сечениями будут кривые 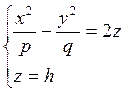 или .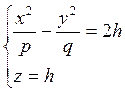

При  в плоскости  получается гипербола 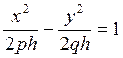. Если , то действительная ось этой гиперболы параллельна оси ОХ, а мнимая параллельна оси ОУ (рис. 7.11). Если  - наоборот. Если , то секущая плоскость есть плоскость ХОУ, а сечение параболоида в этой плоскости имеет уарвнение 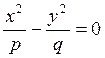 или 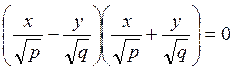. Оно распадется в пару прямых, проходящих через начало координат.

Убедитесь самостоятельно (и сделайте рисунки), что сечения гиперболического параболоида плоскостями, параллельными плоскости XOZ, суть параболы, ветви которых направлены вверх. А сечения плоскостями, паралельными YOZ, - параболы, ветви которых направлены вниз.

§ 7.4. Цилиндры и конус

А. Цилиндры.

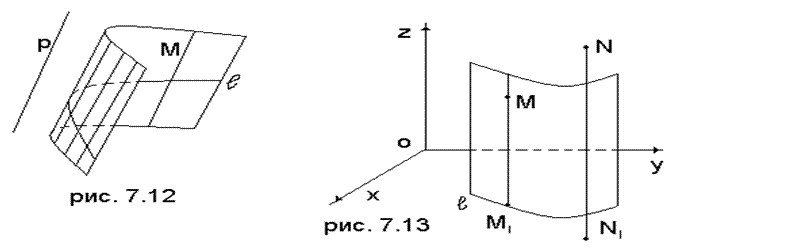
Определение. Цилиндрической поверхностью (или просто – цилиндром) называется поверхность, которая вместе с каждой своей точкой содержит всю прямую, проходящую через эту точку параллельно некторой фиксированной прямой p (рис. 7.12).

Согласно этому определению цилиндр можно представить себе как поверхность, описываемую прямой, которая движется так, что все время остается параллельной фиксированной прямой р. Параллельные прямые, которые составляют цилиндр, называются его образующими; любая кривая на поверхности цилиндра, которая пересекает все образующие, называется его направляющей.

Теорема. Уравнение                                                            (7.4.1)

есть уравнение цилиндрической поверхности с направляющей

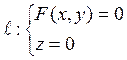                                      (7.4.2)

и образующими, параллельными оси OZ.

Доказательство. Пусть М(х, у, z) – произвольная точка цилиндра с направляющей  и образующими, параллельными оси OZ,  - проекция точки М на плоскость ХОУ (рис. 7.13). Так как координаты точки М₁ удовлетворяют системе (7.4.2), то координаты точки М удовлетворяют уравнению (7.4.1).

Если точка  не лежит на цилиндре, то ее проекция – точка - не принадлежит направляющей  и, следовательно, . Поэтому координаты точки N не удовлетворяют уравнению (7.4.1).

Итак, уравнению (7.4.1) удовлетворяют координаты всех точек цилиндра и только этих точек. Теорема доказана. Она означает, что если в уравнении поверхности отсутствует какая-либо из переменных х, у, z, то данная поверхность есть цилиндр с образующими, параллельными соответствующей оси.

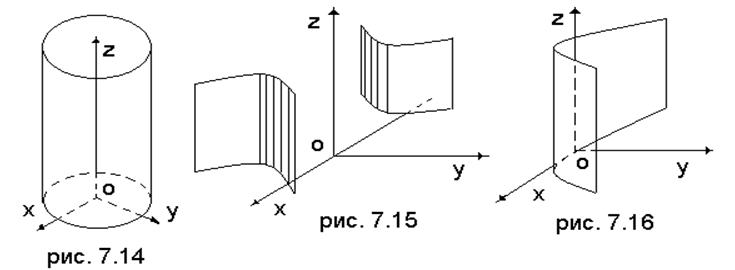
В зависимости от вида направляющей есть три разновидности цилиндров второго порядка – эллиптический (рис. 7.14)

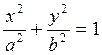                                          (7.4.3)

гиперболический (рис. 7.15)

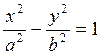                                          (7.4.4)

и параболический (рис. 7.16)

                                              (7.4.5)

Б. Конусы.

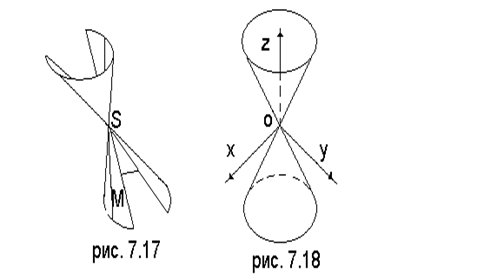
Определение. Канонической поверхностью (или просто – конусом) с вершиной S называется поверхность, которая вместе с каждой своей точкой М содержит всю прямую SM (рис. 7.17).

Согласно этому определению конус можно представить себе как поверхность, описываемую прямой, которая движется так, что все время проходит через вершину. Прямые, которые составляют конус, называются его образующими, любая кривая на  поверхности конуса, которая не проходит через вершину, но пересекает все образующие, называется его направляющей.

В частности, канонической поверхностью будет поверхность вращения прямой. пересекающей ось вращения; такая поверхность называется конусом вращения или прямым круговым конусом. Такую поверхность мы уже встречали в примере § 7.1.

Найдем уравнение конуса вращения, полагая, что прямая 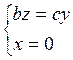, где b и с  - постоянные, вращается около оси OZ.

Уравнение вращающейся прямой в плоскости YOZ - . Согласно § 7.1 уравнение поверхности вращения будет  или

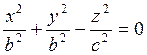                                   (7.4.6)

Призведя теперь сжатие к плоскости YOZ по формулам (7.1.2) и обозначив , получим уравнение более общей поверхности – конуса второго порядка (рис. 7.18):

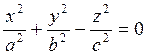                                                                (7.4.6 а)