Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 12

Пример. Путем переноса начала координат упростить уравнение кривой второго порядка .

Решение. Члена с произведением координат в уравнении нет, оба коэффициента при квадратах переменных отличны от нуля. Следовательно, данная квадрика центральная и переносом начала можно уничтожить члены первой степени.

Переносим начало координат в неизвестную пока точку  по формулам . Получаем:  или, после привидения подобных членов, .

          Чтобы уничтожить члены первой степени, полагаем

                           у                           откуда получаем .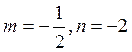

Подсчитываем свободный член:

                                               х 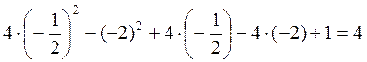      . Итак,

1                                   при переносе начала координат в точку

                              1  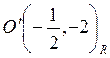                   получаем уравнение

                                                            или .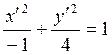

Это – гипербола (ЦН-2). Ее действительная ось имеет длину 2 и расположена по оси

, а мнимая имеет длину 1 и

Рис. 4.34                         расположена по оси  (рис. 4.34).

§ 4.11. Параболические квадрики и их классификация

Определение. Если в уравнении квадрики (4.10.1), которое получается из общего уравнения уничтожением члена с произведением координат, один из коэффициентов  равен нулю, то квадрика называется параболической.

Приступая к изучению параболических квадрик, положим для определенности . Тогда уравнение параболической квадрики будет таким:

                                        (4.11.1)

Вид квадрики существенно зависит от того, равен ли нулю коэффициент , так как при  левая часть уравнения не содержит переменной . Поэтому параболические квадрики разделяются на две разновидности: при  квадрика называется параболической невырожденной (ПН), а при  - параболической вырожденной (ПВ).

Уравнение квадрики ПН можно привести к такому виду: , где 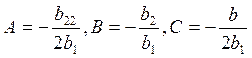. Видим, что  есть квадратичная функция от . Следовательно. Как это известно из школьного курса, данная кривая есть парабола. Ее уравнение переносом начала приведем к каноническому виду. Уравнения переноса начала в неизвестную пока точку  имеют вид .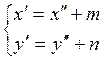

Поэтому уравнение квадрики в новой системе координат  будет  или .

За счет выбора m и n можно избавиться от члена с первой степенью  и от свободного члена. Для этого надо, чтобы m и n удовлетворяли системе уравнений .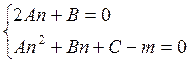

Легко видеть, что эта система имеет единственное решение: из первого уравнения можно найти n, так как , а затем из второго – m.

Таким образом, в системе  квадрика ПН имеет уравнение

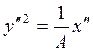                                                      (4.11.2)

Это – парабола с параметром 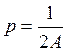, начало координат  находится в вершине параболы.

Уравнение квадрики ПВ получим из (4.11.1), положив :

                                                 (4.11.3)

Обозначив корни трехчлена, стоящего в левой части уравнения, через α и β, мы можем левую часть разложить на множители: . Следовательно, уравнение квадрики распадается в совокупности двух уравнений:  и . Здесь могут представиться три случая.

ПВ-1. Корни α и β – действительные различные. Квадрика представляет собой пару параллельных прямых.

ПВ-2. В случае α = β квадрика представляет собой пару совпавших прямых.

ПВ-3. Корни α и β мнимые, Квадрика называется парой мнимых параллельных прямых. Она не содержит ни одной действительной точки.

Отметим, что в отличие от центральных квадрик, имеющих единственный центр симметрии, параболические либо не имеют центра симметрии (ПН), либо у нее бесконечное множество (ПВ). Поэтому параболические квадрики иногда называют нецентральными.

§ 4.12. Классификация квадрик (сводка результатов). Примеры.

В § 4.9 – 4.11 мы нашли все виды кривых, которые задаются общим уравнением второй степени (4.9.1). Результаты сведем в таблицу. При этом будем пользоваться обозначениями предыдущих параграфов: Ц – центральная квадрика, П – параболическая, Н- невырожденная квадрика. В – вырожденная.