Решение.
Так как 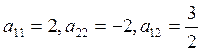 , то уравнение (4.9.3) для
определения угла поворота имеет вид
, то уравнение (4.9.3) для
определения угла поворота имеет вид 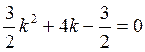 или
или ![]() Оно имеет корень
Оно имеет корень 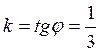 .
Синус и косинус угла поворота теперь находим из системы
.
Синус и косинус угла поворота теперь находим из системы 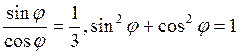 .
Эта система имеет решение
.
Эта система имеет решение 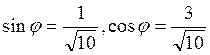 . Поэтому уравнения
поворота имеют следующий вид:
. Поэтому уравнения
поворота имеют следующий вид: 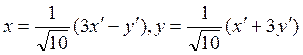 .
.
Далее
находим уравнение квадрики в новой системе координат 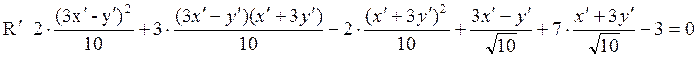 или
после упрощений
или
после упрощений 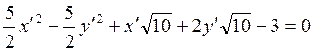 .
.
Так
как в уравнении присутствуют квадраты обеих переменных, квадрика центральная.
Переносим начало координат по формулам ![]() и
получаем уравнение квадрики в системе
и
получаем уравнение квадрики в системе ![]() :
:
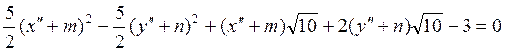 или
или
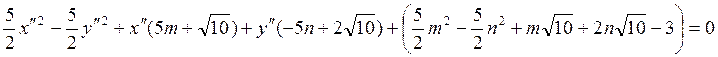
Теперь
выбираем m и n так, чтобы члены первой степени уничтожились: 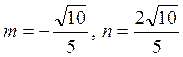 . Мы нашли координаты нового начала (центра
квадрики):
. Мы нашли координаты нового начала (центра
квадрики): 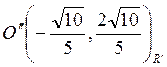 .
.
Далее подсчитываем свободный член в уравнении квадрики:
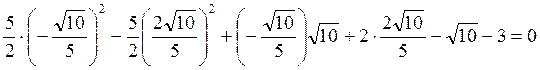 и получаем ее уравнение в системе
и получаем ее уравнение в системе ![]() :
: 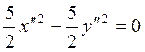 или
или ![]() .
.
Получилась пара прямых ![]() и
и ![]() , пересекающихся в точке
, пересекающихся в точке ![]() .
.
Выполняем
чертеж. Ось ![]() проходит по прямой ОК, К(3, 1), так как
угол наклона этой прямой совпадает с углом наклона оси
проходит по прямой ОК, К(3, 1), так как
угол наклона этой прямой совпадает с углом наклона оси ![]() .
Остальные построения в пояснениях не нуждаются.
.
Остальные построения в пояснениях не нуждаются.
ЧАСТЬ 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
ГЛАВА 5. ВЕКТОРЫ И КООРДИНАТЫ В ПРОСТРАНСТВЕ
§ 5.1. Компланарные векторы. Разложение вектора на составляющие
В настоящей главе понятия координат и вектора распространяется на трехмерное пространство. При этом оказывается, что многие понятия и свойства, изученные в первых двух главах нашего курса, переносятся на трехмерное пространство без изменений или с небольшими очевидными коррективами. Разумеется, возникают и новые понятия.
Безо всяких изменений на трехмерное пространство переносятся понятия и свойства, не связанные с координатами: определение вектора (§ 2.1), сложение и вычитание векторов, умножение вектора на число, а также свойства этих действий (§§ 2.2 и 2.3). Теорема § 2.4 о разложении произвольного вектора на составляющие по двум неколлинеарным векторам верна только в том случае, когда все три вектора можно расположить в одной плоскости.
Для обобщения этой теоремы введем новые понятия.
Определение. Три или более векторов называются компланарными, если они параллельны одной плоскости.
Если компланарные векторы отложить от одной точки, то они расположатся в одной плоскости. Некомпланарные векторы этим свойством не обладают.
На рис. 5.1 ABCDA1B1C1D1 – параллелепипед, M и N – середины боковых ребер AA1 и BB1.
Тройка
векторов ![]() компланарна, так как все векторы
параллельны основаниям параллелепипеда.
компланарна, так как все векторы
параллельны основаниям параллелепипеда.
Тройка
![]() компланарна по той же причине.
компланарна по той же причине.
Тройка
![]() не компланарна, так как всякая плоскость,
параллельная первым двум, параллельна основаниям, а третий вектор им не параллелен.
не компланарна, так как всякая плоскость,
параллельная первым двум, параллельна основаниям, а третий вектор им не параллелен.
Очевидно, что если в тройке векторов есть два коллинеарных, то такая тройка компланарна, так как при приведении таких векторов к общему началу они располагаются в одной плоскости (рис. 5.2). В частности, если в тройке есть нулевой вектор, то тройка компланарна.
Определение.
Пусть ![]() - векторы,
- векторы, ![]() -
действительные числа. Тогда вектор
-
действительные числа. Тогда вектор
![]() (5.1.1)
(5.1.1)
называется линейной комбинацией данных векторов; данные числа называются коэффициентами линейной комбинации. C

![]()

 D1
B1
D1
B1
![]()
![]()
![]()

![]()
![]() C1
C1 ![]()
![]()
![]()
![]() A1
A1
![]()
 М
B1
М
B1 ![]() B
B ![]()
![]()
![]()
![]()
![]()
![]() D N
D N ![]()
![]() C
C
![]() A B
A B
![]()
![]()
![]()
![]() A A1
A A1
Рис. 5.1 Рис. 5.2 Рис. 5.3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.