Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 21

Следствие 4. (перестановка сомножителей). При циклической перестановке векторов в тройке ее смешанное произведение остается без изменения, а при перестановке только двух векторов оно меняет знак:

             (5.6.3)

Пример. Докажите, что .

Решение. В силу следствия 4 .

§ 5.7. Дистрибутивность векторного произведения.

Векторное и смешанное произведения в координатах

В § 5.5, доказав пять свойств векторного произведения, мы остановились перед дистрибутивностью.

Свойство 6. (дистрибутивность). Векторное произведение дистрибутивно относительно сложения:

                                    (5.7.1)

Доказательство. Рассмотрим скалярное произведение произвольного вектора  на вектор . Это произведение по определению есть смешанное произведение векторов ,  и , которое мы преобразуем, воспользовавшись следствием 4 из теоремы о геометрическом смысле смешанного произведения: . Получилось скалярное произведение векторов  и .

Как известно (§ 2.7), скалярное произведение обладает дитрибутивностью относительно сложения. Поэтому цепочку равенств можно продолжить: . Снова воспользуемся следствием 4: . Итак, для произвольного вектора  верно равенство .

Снова воспользуемся дистрибутивностью скалярного произведения: . Если теперь обозначить , то . Так как последнее равенство верно при любом , то оно верно, в частности, при . Поэтому , откуда , а это равносильно равенству (5.7.1), которое надо доказать.

Векторное произведение в координатах. Вычислим векторное произведение вектора  на вектор .

Так как  и , то в дистрибутивности

.

Числовые множители можно вынести за знак векторного произведения (§ 5.5, свойство 5), поэтому . Подставляем сюда вычисленные ранее произведения базисных векторов (§ 5.5, свойство 4): . Полученную формулу векторного произведения запишем в удобном для запоминания виде:

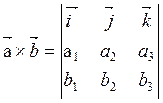                                (5.7.2)

Мы получили выражение векторного произведения в координатах. Используя свойства определителей, их этой формулы можно легко вывести ранее установленные факты: антикоммукативность векторного произведения (§ 5.5, свойство 3) и условие коллинеарности векторов (§ 5.5, свойство 2).

Смешанное произведение в координатах. Вычислим смешанное произведение векторов.

По формуле (5.7.2) .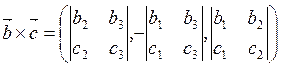

Смешанное произведение  - это скалярное произведение векторов  и . Находим его по формуле скалярного произведения (5.2.3):

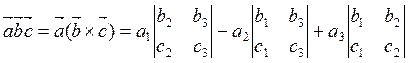 и окончательно смешанное произведение в координатах записывается так:

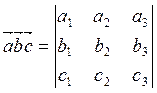                                           (5.7.3)

Используя правило перестановки строк в определителе, из полученной формулы можно легко вывести правила перестановок сомножителей в смешанном произведении, которые были получены в § 5.6 (следствие 4). Там же (следствие 3) было показано, что условие компланарности трех векторов заключается в равенстве нулю их смешанного произведения; на основании формулы (5.7.3) это приводит нас к ранее выведенному условию компланарности (5.2.2).

Выражения векторного и смешанного произведений в координатах эффективно применяются в аналитической геометрии.

Задача 1. Найти площади параллелограмма и треугольника, построенных на векторах  и .

Решение. По свойству 1 векторного произведения (§ 5.5) площадь параллелограмма выражается формулой . В силу (5.7.2) 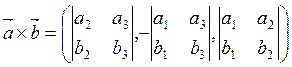, поэтому

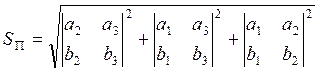                (5.7.4)

А так как площадь треугольника S_Т равна половине площади параллелограмма, построенного на тех же векторах, что и треугольник,

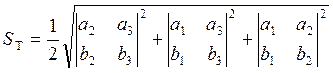              (5.7.5)

Важный частный случай последней формулы будет, когда треугольник находится в плоскости ХОУ. В этом случае , и под корнем два слагаемых обращаются в нуль. Получается

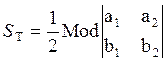                                         (5.7.6)

Пусть известны координаты вершин треугольника на плоскости ХОУ: А(х₁,у₁), В(х₂, у₂), С(х₃, у₃). Этот треугольник можно рассматривать как треугольник в пространстве, построенный на векторах  и . Его площадь находим по формуле (5.7.6): 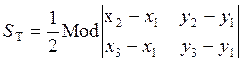. Вычисляя определители, убеждаемся, что эта формула равносильна ранее полученной формуле (1.2.5), вывод которой в § 1.2 неполный.