Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 30

В § 7.1 будут рассмотрены некторые вспомогательные вопросы, в § 7.2-§ 7.4 мы выведем канонические уравнения всех действительных пространственных квадрик, не распадающихся в пару плоскостей, а в § 7.5 и § 7.6 полученные уарвнения используем для изучения геометриечских свойств квадрик.

§ 7.1. Вспомогательные вопросы

А. Поверхность вращения.

          Определение. Поверхностью вращения кривой (образующей) около прямой (оси) называется поверхность, которая вместе с каждой точкой образующей содержит всю окружность (паралель), проходящую через эту точку, расположенную в плоскости, перпендикулярной оси, и имеющую центр на оси. Сечение поверхности плоскостью, проходящей через ось, называется меридианом.

Через каждую точку поверхности вращения, не лежащую на оси, проходит одна параллель и один меридиан.

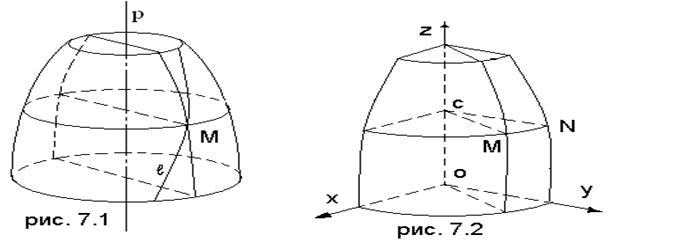
На рис. 7.1  - образующая, р – ось вращения, М – точка поверхности. Показаны параллель и меридиан, проходящие через эту точку. Обратите внимание, что образующая – не обязательно плоская кривая. Вообще, за образующую можно принять любую кривую, лежащую на поверхности вращения, если она пересекает все параллели. В частности, можно считать образующей любой меридиан.

Задача. Пусть в плоскости YOZ расположена кривая . Найти уравнение поверхности вращения этой кривой около оси OZ. Зметим, что в пространстве данная кривая определяется системой двух уравнений .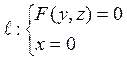

Решение. На рис. 7.2  -данная кривая (образующая), М(х, у, z) - произвольная точка поверхности вращения, N – точка образующей, лежащая на одной параллели с М, С –центр параллели, СМ и CN – радиусы параллели; .

Определим координаты точки N. Так как она лежит в плоскости YOZ, то . А так как , то . И, наконец, из параллельности плоскости ХОУ и плоскости, в которой находится параллель, следует, что аппликаты точек М и N равны: . Итак, . Но поскольку , то

                                        (7.1.1)

Это уравнение выражает зависимость между координатами произвольной точки поврехности вращения, поэтому оно является уравнением поверхности вращения.

Вывод: если в плоскости YOZ дано уравнение образующей, а осью вращения служит ось OZ, то уранение поверхности вращения получим, заменив в уравнении образующей переменную у на .

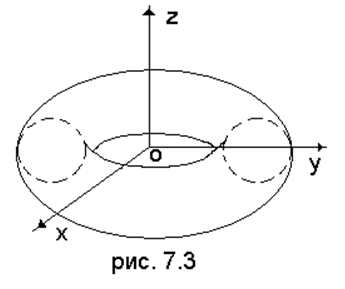                                                                                          Пример 1. Найдите уранвнеие поверхности вращения окружности 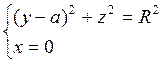, около оси OZ; эта поверхность называется тором (смотри рис. 7.3).

Решение. В соответствии со сделаннымвыше выводом уравнение тора получим, если в уравнении окружности  заменим на

. Отсюда  и окончательно

Пример 2. Найдите уравнение поверхности вращения прямой 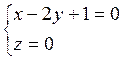, около оси ОУ.

Решение. В этом случае образующая поверхность вращения в плоскости ХОУ имеет уравнение . Теперь надо х заменить на : . После упрощений получаем .

Б. Сжатие.

Определение. Сжатием к плоскости α с коэффициентом  называется такое преобразование пространства, при котором каждая точка пространства смещается по перпендикуляру к плоскости α, а ее расстояние до плоскости изменяется в k раз.

На рис. 7.4 образом точки М является точка  и при этом , где С – основание перпендикуляра, опущенного из М на α. Из определения ясно, что все точки плоскости α неподвижны.

Заметим, что при  сжатие представляет собой тождественное преобразование, а при  сжатие к плоскости вполне уместно было бы назвать растяжением от плоскости. Для простоты дальнейших формулировок мы ограничимся одним термином – сжатие.

Если плоскость α совпадает с координатной плоскостью YOZ, то координаты произвольной точки М(х, у, z)  и ее образа  связаны очевидными соотноешниями

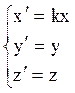                                               (7.1.2)

(рис. 7.5). Это и есть уравнения сжатия к плоскости YOZ.

Найдем образ произвольной плоскотси  при сжатии. Применяя уравнения сжатия, находим уравнение этого образа: 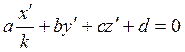. Так как получилось уарвнение первой степени, то отсюда заключаем, что при сжатии плоскость переходит в плоскость. А так как прямая есть линия пересечения плоскостей, то при сжатии прямая переходит в прямую.