Определение. Ненулевой вектор называется направляющим вектором плоскости, если он ей параллелен или лежит в ней.
Пусть
неколлинеарные векторы ![]() и
и ![]() -
направляюще векторы плоскости α (рис. 6.2). Тогда любой вектор, компланарный с
ними, тоже является направляющим для этой плоскости, так как все три вектора,
если их построить из одной точки, располагаются в плоскости, параллельной α. Но
любой вектор, компланарный векторам
-
направляюще векторы плоскости α (рис. 6.2). Тогда любой вектор, компланарный с
ними, тоже является направляющим для этой плоскости, так как все три вектора,
если их построить из одной точки, располагаются в плоскости, параллельной α. Но
любой вектор, компланарный векторам ![]() и
и ![]() , может быть разложен на составляющие по
этим векторам (см. § 2.4, а также § 5.1). Поэтому все направляющие векторы
плоскости α можно представить в виде
, может быть разложен на составляющие по
этим векторам (см. § 2.4, а также § 5.1). Поэтому все направляющие векторы
плоскости α можно представить в виде ![]() , где
, где ![]() .
.
Точка плоскости и два ее направляющих вектора определяют плоскость. Поэтому следующая задача имеет единственное решение.
Задача
2. Найти уравнение плоскости α по точке ![]() и
неколлинеарным направляющим векторам
и
неколлинеарным направляющим векторам ![]() и
и ![]() .
.
Решение.
Для наглядности векторы ![]() и
и ![]() построим из одной точки А, тогда они
расположатся в плоскости α (рис. 6.3). Пусть М(х, у, z) – какая-либо
точка. Она принадлежит плоскости α тогда и только тогда, когда векторы
построим из одной точки А, тогда они
расположатся в плоскости α (рис. 6.3). Пусть М(х, у, z) – какая-либо
точка. Она принадлежит плоскости α тогда и только тогда, когда векторы ![]() ,
, ![]() ,
, ![]() компланарны. Согласно теореме § 5.2
условие компланарности этих векторов имеет вид
компланарны. Согласно теореме § 5.2
условие компланарности этих векторов имеет вид
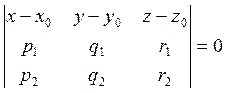 (6.1.2)
(6.1.2)
Это
и есть искомое уравнение плоскости по точке и двум направляющим векторам.
Читателю необходимо продумать, какое значение имеет неколлинеарность
направляющих векторов ![]() и
и ![]() .
.
При
тех же данных можно получить уравнение плоскости в другом виде, если воспользоваться
разложением вектора ![]() по векторам
по векторам ![]() и
и ![]() . Имеем:
. Имеем:
![]() .
.
Отсюда:
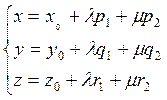 (6.1.3)
(6.1.3)
Это – параметрические уравнения плоскости. λ и μ – переменные параметры.
Из
уравнения (6.1.2) легко получается уравнение плоскости по трем точкам ![]() не лежащим на одной прямой. Для этого
достаточно записать ее уравнение по точке, например, А и двум неколлинеарным
направляющим векторам, например,
не лежащим на одной прямой. Для этого
достаточно записать ее уравнение по точке, например, А и двум неколлинеарным
направляющим векторам, например, ![]() и
и ![]()
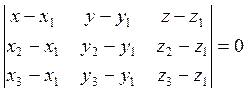 (6.1.4)
(6.1.4)
Это уравнение равносильно такому:
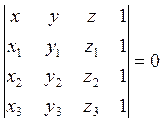 (6.1.5)
(6.1.5)
что можно проверить непосредственным подсчетом определителей или сведением одного к другому путем элементарных преобразований; второй путь приводит к цели быстрее.
Пример 1. Найдите уравнение плоскости, проходящей через ось ординат и точку А(1, 2, 2).
Решение.
Уравнение искомой плоскости находится по точке О(0, 0, 0) и направляющим
векторам ![]() и
и ![]() (рис.
6.4):
(рис.
6.4): 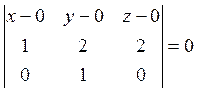 или, после вычислений,
или, после вычислений, ![]() .
.
Пример
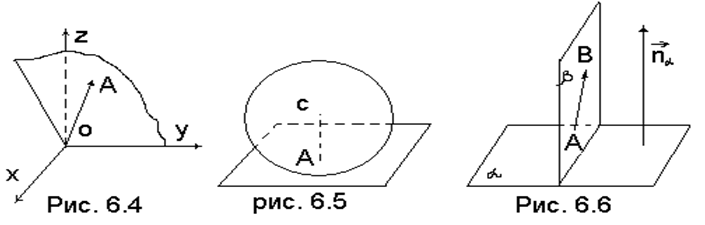
2. Найдите уравнение плоскости, которая касается сферы ![]() в точке А(3, -3, 2).
в точке А(3, -3, 2).
Решение. Непосредственной подстановкой убеждаемся, что данная точка действительно лежит на сфере.
Из
уравнения сферы находим ее центр С(1, -2, 4). Вектор ![]() -
нормальный вектор искомой плоскости (рис. 6.5). Поэтому ее уравнение можно
найти по точке А и нормальному вектору
-
нормальный вектор искомой плоскости (рис. 6.5). Поэтому ее уравнение можно
найти по точке А и нормальному вектору ![]() :
: ![]() , откуда после упрощений получаем
окончательно
, откуда после упрощений получаем
окончательно ![]() .
.
 Пример 3. Через точки А(3, 2, -2) и
В(0, 1, 1) проведена плоскость перпендикулярно плоскости
Пример 3. Через точки А(3, 2, -2) и
В(0, 1, 1) проведена плоскость перпендикулярно плоскости ![]() . Найдите ее уравнение.
. Найдите ее уравнение.
Решение.
Первый способ. Нормальный вектор ![]() данной
плоскости α имеет координаты (1, 1, 1). Так как и он, и искомая плоскость β
перпендикулярны плоскости α (рис. 6.6), то
данной
плоскости α имеет координаты (1, 1, 1). Так как и он, и искомая плоскость β
перпендикулярны плоскости α (рис. 6.6), то ![]() и,
следовательно,
и,
следовательно, ![]() есть направляющий вектор
плоскости β. Другой направляющий вектор этой плоскости – это вектор
есть направляющий вектор
плоскости β. Другой направляющий вектор этой плоскости – это вектор ![]() . Теперь уравнение искомой плоскости
находится по точке А (или В) и двум направляющим векторам:
. Теперь уравнение искомой плоскости
находится по точке А (или В) и двум направляющим векторам: 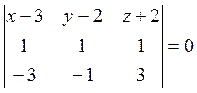 . Отсюда после упрощений получаем
. Отсюда после упрощений получаем ![]() .
.
Второй
способ. Вектор ![]() по определению векторного
произведения (§ 5.5) перпендикулярен обоим перемножаемым векторам, поэтому он
перпендикулярен искомой плоскости β, то есть является для нее нормальным
вектором. По формуле (5.7.2)
по определению векторного
произведения (§ 5.5) перпендикулярен обоим перемножаемым векторам, поэтому он
перпендикулярен искомой плоскости β, то есть является для нее нормальным
вектором. По формуле (5.7.2) 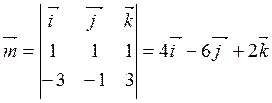 .
.
Итак,
![]() , Вектор
, Вектор ![]() нормальный
вектор плоскости β. Уравнение этой плоскости находим по точке В и нормальному
вектору
нормальный
вектор плоскости β. Уравнение этой плоскости находим по точке В и нормальному
вектору ![]() (формула (6.1.1)):
(формула (6.1.1)): ![]() или
или
![]() .
.
§ 6.2. Общее уравнение плоскости и его частные случаи
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.