Достаточность. Эту часть доказательства получим, если доказательство необходимости проследим в обратном направлении - от конца к началу.
Скалярное
произведение двух векторов в пространстве определяется точно так же, как и на
плоскости (§ 2.7). Все бескоординатные свойства остаются в силе, а свойства,
связанные с координатами, выводятся так же, как и прежде. И отличаются лишь
присутствием третьей координаты. А именно, скалярное произведение векторов ![]() и
и ![]() выражается
формулой
выражается
формулой
![]() (5.2.3)
(5.2.3)
Длина
вектора ![]() равна
равна
![]() (5.2.4)
(5.2.4)
а
угол φ между векторами ![]() и
и ![]() определяется
формулой
определяется
формулой
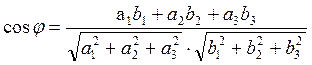 (5.2.5)
(5.2.5)
Подчеркнем, что последние три формулы верны только в прямоугольных декартовых координатах.
Как
и в двумерном случае (§ 2.6), проекции вектора на координатные оси равны его
координатам. А именно, если ![]() , то
, то
![]() (5.2.6)
(5.2.6)
Определение. Косинусы углов, которые вектор образует с осями прямоугольной декартовой системы координат, называются направляющими косинусами вектора.
Из последних формул с учетом формулы (5.1.4) получаем
![]() (5.2.7)
(5.2.7)
Где
α, β, γ – углы вектора ![]() с осями координат. Мы выразили
координаты вектора через его длину и направляющие косинусы.
с осями координат. Мы выразили
координаты вектора через его длину и направляющие косинусы.
По
формуле (5.2.4) ![]() , поэтому
, поэтому
![]() (5.2.8)
(5.2.8)
То есть сумма квадратов направляющих косинусов произвольного вектора равна 1.
Рассмотрим
орт вектора ![]() , то есть единичный вектор
, то есть единичный вектор ![]() сонаправленный с вектором
сонаправленный с вектором ![]() . По формулам (5.2.7)
. По формулам (5.2.7) 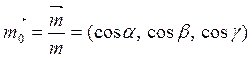 , и мы приходим к выводу: направляющие
косинусы любого вектора равны координатам его орта.
, и мы приходим к выводу: направляющие
косинусы любого вектора равны координатам его орта.
Пример. Вектор длины 6 образует с осями ОХ и ОУ углы по 600. Определить координаты вектора и угол, который он образует с осью OZ, если известно, что этот угол тупой.
Решение.
Сначала найдем направляющие косинусы вектора. Имеем: 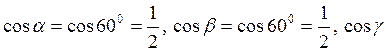 найдем из формулы (5.2.8):
найдем из формулы (5.2.8): 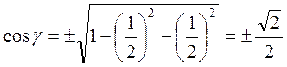 .
.
Так
как по условию угол γ тупой, то ![]() и
и 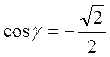 . Следовательно, γ = 1350.
. Следовательно, γ = 1350.
Мы
нашли угол вектора с осью аппликат. Координаты вектора найдем по длине и направляющим
косинусам, воспользовавшись формулами (5.2.7): ![]() .
.
§ 5.3. Координаты точки. Геометрический смысл уравнений
между координатами.
Определение. Координатами точки в аффинной (и, в частности, - в прямоугольной декартовой) системе координат называются координаты ее радиус-вектора.
Таким
образом, по определению координаты точки М равны координатам вектора ![]() .
.
На
рис. 5.7 показано построение точки А(-2, -2, 1); в соответствии с определением
строится ее радиус-вектор ![]() . Как и на плоскости, координаты
вектора равны разностям соответствующих координат концов: если A(x1, y1, z1) и В(x2, y2, z2), то
. Как и на плоскости, координаты
вектора равны разностям соответствующих координат концов: если A(x1, y1, z1) и В(x2, y2, z2), то ![]() . Это позволяет простейшие (и в то же время
– важнейшие) формулы аналитической геометрии на плоскости распространить на
трехмерное пространство. Это формула длины отрезка:
. Это позволяет простейшие (и в то же время
– важнейшие) формулы аналитической геометрии на плоскости распространить на
трехмерное пространство. Это формула длины отрезка:
![]() (5.3.1)
(5.3.1)
и формулы деления отрезка АВ в отношении λ:
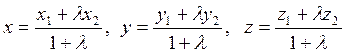 (5.3.2)
(5.3.2)
Первая из этих формул вытекает из (5.2.4) и верна только в прямоугольных декартовых координатах, вторые выводятся как в § 2.5, они верны в произвольных аффинных координатах. В дальнейшем для простоты и определенности мы будем пользоваться только прямоугольными декартовыми координатами, если нет специальной оговорки.
Уравнение относительно координат
![]() (5.3.3)
(5.3.3)
определяет в пространстве, вообще говоря, некоторую поверхность; ей принадлежат те и только те точки, координаты которых удовлетворяют уравнению. Подтвердим это простыми примерами.
Пример 1. Уравнение z = 0 – это уравнение координатной плоскости ХОУ.
![]()
![]() Z
Z Z
Z
Z Z

![]()
![]()
![]()
![]()
![]()
 A М
A М
![]()
![]()
![]()
![]()
![]() · M
· M
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.