Понятие системы связи, сети связи, страница 60

Из (7) следует, что если к многочлену A(X) прибавить остаток от деления A(X) на g(X), то получим многочлен A(X)+R(X) степени не выше n-1, делящийся на g(X) без остатка. Комбинация, соответствующая этому многочлену, является комбинацией циклического кода и содержит информационные символы, предоставленные многочленом A(X).

Разделяют 2 алгоритма деления одного многочлена на другой.

К первому относят такой алгоритм, когда к началу деления известны по крайней мере r старших степеней делимого и на каждом шаге в процесс деления вовлекается лишь одна следующая степень делимого.

Ко второму алгоритму относят такой, когда к началу деления известна лишь одна старшая степень делимого и в процесс деления на каждом шаге вовлекается лишь одна следующая степень делимого.

Поскольку алгоритмы деления несколько различаются, то будут несколько различаться и устройства, обеспечивающие эти алгоритмы деления.

Второй способ построения комбинаций циклического кода

 Основан на использовании проверочного многочлена h(X). При этом способе проверочные символы находятся как скалярные произведения двух k-элементных последовательностей, одна из которых является изменяемой и строится на базе коэффициентов многочлена A(X), а вторая является неизменной и представляет собой коэффициенты многочлена  

Прибавление одночлена  убирает старшую степень в многочлене (получается степень k).

В теории циклических кодов доказано, что старший проверочный символ

Второй проверочный символ:

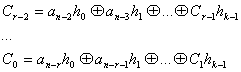
37. Кодеры циклических кодов

Деление одного многочлена на другой аппаратно выполняется при помощи регистра сдвига с обратными связями, где элементы сложения по модулю два располагаются между элементами памяти. Различие алгоритмов деления приводит к некоторому различию схем таких регистров. Регистр, реализующий первый алгоритм деления, называется регистром 1 (Рг1), а реализующий второй алгоритм деления – регистром 2 (Рг2).