Понятие системы связи, сети связи, страница 50

Заметим, что количество комбинаций синдрома 2^r всегда меньше, чем число векторов ошибок 2ⁿ, т.к. r<n. С другой стороны, как видно из формулы (11) вид комбинации синдрома определяется вектором ошибок. Это означает, что соответствие между вектором ошибок и комбинациями синдрома однозначно, но не взаимнооднозначно, т.е. несколько векторов ошибок порождают одну и ту же комбинацию синдрома. Эта ситуация характеризуется следующим графом:

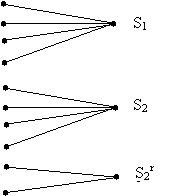Выясним сколько различных векторов ошибок порождают одну и ту же комбинацию синдрома. Для этого найдем комбинацию синдрома, порожденную вектором ошибок e, который можно рассматривать как сумму по модулю 2 одной из ненулевых последовательностей g = (g₁…g_n), не совпадающей ни с одной из комбинаций кода и с 1 из комбинаций линейного кода

Рассмотрим вектор ошибок, равный    .

Вектор ошибок е не является комбинацией линейного кода, т.к. сумма 2-х последовательностей длины n дает комбинацию линейного кода только тогда, когда обе последовательности принадлежат линейному коду, что противоречит выбору g.

Найдем синдром вектора ошибок e.

    (12)

т.е. синдром вектора ошибок e определяется только последовательностью g, не являющейся комбинацией кода.

Поскольку комбинаций линейного кода 2^k, то может быть получено ровно 2^k векторов е, дающих одну и ту же комбинацию синдрома, следовательно, ровно 2^k векторов ошибок порождают одну  ту же комбинацию синдрома.

Очевидно, что число групп, каждая из которых состоит из 2^k векторов ошибок столько, сколько комбинаций синдрома, т.е. 2^r. Во все эти группы входят все вектора ошибок, т.к. в каждую группу входит 2^k: