Понятие системы связи, сети связи, страница 33

Эта задача решается в 2 этапа:

1 этап: Определение минимальной разрядности n_min корректирующего кода

2 этап: Нахождение вида самих комбинаций.

Обычно эти этапы осуществляются раздельно.

Определение минимальной разрядности корректирующего кода

Точное решение этой задачи известно не для всех возможных случаев. Однако существует несколько способов, позволяющих определить область, в которой содержится решение.

Воспользовавшись способом, предложенным А.А. Харкевичем.

Если известно число E_и векторов ошибок, подлежащих исправлению, то очевидно любой из них должен исправляться в любой из N комбинаций кода. Отсюда число случаев, когда ошибки должны исправляться E_иN.

При любом разбиении множества запрещенных комбинаций на подмножества A_i ошибки будут исправляться правильно всего в (N₀-N) случаях. Поэтому для исправления ошибок необходимо выполнить условия:            

После элементарных преобразований окончательно получим:

                (9)

Пусть в коде должны исправляться все ошибки кратности от 1 до ν_и, тогда число ν_и случаев исправления ошибок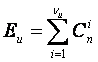   

Подставив, E_и  в формулу (9) и учитывая, что N₀=2ⁿ, окончательно получим:

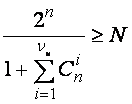              (10)

Нетрудно видеть, что левая часть неравенства (10) зависит от n.

Подставляя в формулу (10) различные значения n, находим  минимальное n, при котором неравенство удовлетворяется.

Это значение n, равное n_гр, определяет нижнюю границу области минимальной разрядности корректирующего кода, позволяющего исправлять ошибки кратности от 1 до ν_и.

Если n<n_гр, то принципиально не существует код разрядности n, исправляющий E_и векторов ошибок.

Если n=n_гр, то существует код, исправляющий E_и векторов ошибок. Но не всегда кратность исправляемых ошибок лежит в интервале от 1 до ν_и. Поэтому может оказаться, что для некоторых случаев код, позволяющий исправлять все ошибки с кратностью от 1 до ν_и, имеет минимальную разрядность n_min>n_гр.