Понятие системы связи, сети связи, страница 46

Пример: Построить порождающую матрицу G в форме (1) линейного (7,4)-кода, задаваемым набором коэффициентов C_ji

Решение:

См. страницу 77

26. Способы построения комбинаций линейных кодов

Различают 3 способа построения комбинации линейных кодов:

1. проверочные символы находятся как сумма по модулю два определенных информационных символов (смотри первое определение линейного кода). Затем найденные проверочные символы приписываются к информационным.

В результате получаем  V=(a_1...a_k b₁­_… b­_r);

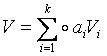2. комбинации линейного кода находятся как сумма по модулю два соответствующих строк матрицы G в канонической форме. Если через V_i (где i = 1,…k) обозначить i – тую строку матрицы G, а через A=(a_1...a_k) комбинацию информационных символов, то комбинация линейного кода, содержащая А, может быть получена так:

         (2)

3. комбинации линейного кода находятся, путем умножения комбинаций информационных символов А на порождающую матрицу G по правилу умножения матриц, с той лишь особенностью, что нахождение элементов в матрице – строке, являющейся произведением, обычное сложение заменяется на сумму по модулю два.

Обычно это записывается так:

        (3)

V,A – матрица – строка

G – порождающая матрица

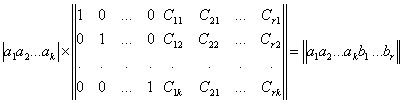     (1)

Докажем, что сумма по модулю любых двух комбинаций кода так же является комбинацией этого кода

Пусть имеется 2 кодовых комбинации

Сложим и по модулю 2