Понятие системы связи, сети связи, страница 59

    (6)

Пример:

Построить проверочную матрицу Н_ц циклического (7, 4)-кода, порождаемого многочленом .

Найдем проверочный многочлен h(X):

Многочлен строк матрицы Н_ц:

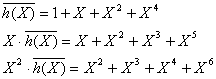                 т.к. r = 3

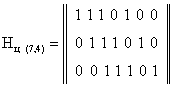
36. Способы построения комбинаций циклических кодов

Для образования комбинаций циклических кодов применяются 2 способа.

Первый основан на использовании порождающего многочлена g(X), а второй – на использовании проверочного многочлена h(X).

Прежде чем рассматривать первый способ, выполним следующие рассуждения:

любой многочлен  V(X), представляющий комбинацию циклического кода, будем рассматривать как сумму двух многочленов A(X) и R(X), т.е. V(X) = A(X) + R(X),

где A(X) – многочлен, представляющий информационные символы, стоящие на первых k позициях комбинации,

R(X) -  многочлен, представляющий проверочные символы, стоящие на последних r позициях в комбинации.

Многочлен A(X) не имеет степеней ниже n-k=r, а многочлен R(X) – степеней выше, чем r-1.

Обозначим многочлен, представляющий k информационных символов через

Для того, чтобы получить многочлен A(X), необходимо , т.е.

Первый способ построения комбинаций циклического кода

сводится по существу к нахождению многочлена R(X), если известен  многочлен A(X)

Разделим A(X) на g(X), получим частное A(X) и остаток R(X). В соответствии с алгоритмом деления Евклида можно записать

Прибавим к обеим частям равенства R(X)

            (7)