Понятие системы связи, сети связи, страница 53

                                                     было

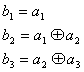
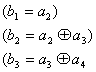
При использовании для описания линейных кодов ТМ укорочения кода не один символ сводится к исключению из матрицы G первой строки первого столбца в результате чего появляется новая матрица G_y размера (k-1)x(n-1).

Эта матрица порождает укороченный линейный код с 2^k-1 комбинациями. В матрице Н укорочение кода на 1 символ сопровождается исключением первого столбца.

Пример:

Построить порождающую и проверочную матрицы линейного (6,3)-кода, полученного в результате укорачивания на 1 символ линейного (7,4)-кода, задаваемого 1-м набором коэффициентов C_ji.

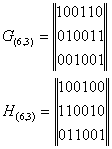
Проведя укорочение на 1 символ (n-1,k-1)-кода, получим новый укороченный (n-2,k-2)-код.

33. Второе определение циклического кода. Порождающий многочлен циклического кода.

Пусть имеем линейный (n, k)-код, являющийся циклическим. Рассмотрим все его ненулевые комбинации и соответствующие многочлены. Найдем комбинацию, многочлен которой имеет наименьшую степень. Ею может быть только последняя строка матрицы G, т.к. комбинация линейного кода отлична от нуля только тогда, когда отличен от «0» хотя бы один информационный символ.

      Среди всех комбинаций с одним отличным от «0» информационным символом многочленом наименьшей степени будет представляться последняя строка матрицы G как имеющая «1» в младшем информационном символе.

      Обозначим многочлен, представляющий последнюю строку матрицы G через g(X). Нетрудно видеть, что это многочлен степени r. Выполним последовательно k-1 циклических сдвигов комбинации, представляемой многочленом g(X). Учитывая цикличность комбинации циклического кода,  получим помимо исходной еще k-1 комбинацию циклического кода. Всем этим комбинациям соответствуют многочлены g(X), Xg(X)…X^k-1g(X).

   Поскольку степени всех указанных многочленов различны, то полученные комбинации линейно независимы. Представляющие их многочлены вместе с многочленами, получаемыми при сложении их по 2, по 3 и т.д. до всех k, образуют множество из 2^k-1 многочленов. Первой особенностью этого множества является о, что среди них нет такого, степень которого бы превышала n-1 (k-1+r = n-1), а второй – то, что каждый из них делится без остатка на g(X).