Как видно из таблицы, порождающий многочлен может представлять собой непрерывный многочлен или произведение непрерывных многочленов, как одинаковых, так и разных степеней.
Структура и степень g(X) полностью определяют свойства и корректирующую способность порождаемого или циклического кода
34. Порождающая матрица циклического кода
Знание порождающего многочлена позволяют легко построить порождающую матрицу Gц циклического кода. В качестве строк этой матрицы обычно берутся коэффициенты k многочленов g(X), Xg(X),…, Xk-1 g(X). Поскольку степени этих многочленов различны, то строки матрицы Gц линейно независимы. Матрица Gц записывается так:
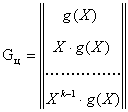
Складывая строки матрицы Gц по две, по три и, наконец, все вместе получим все оставшиеся 2k – k – 1 ненулевые комбинации циклического кода.
Пример:
Построить порождающую матрицу циклического (7, 4) – кода с порождающим многочленом g(X) = X3 + X +1. Заметим, что
k = r + 1 = 4.
Многочлены строк:
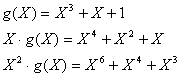
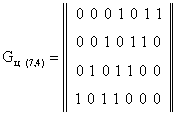
При сравнении матрицы Gц с матрицей G линейного кода видно, что они не совпадают. Однако используя элементарные операции над строками, матрицу Gц можно привести к матрице G. К элементарным операциям над строками матрицы относятся следующие 3:
В теории матриц доказано, что если одна матрица получается из другой в результате последовательного применения элементарных операций над строками, то пространство строк этих двух матриц совпадает. Следовательно, матрица G, полученная из матрицы Gц, порождает тот же циклический код, что и матрица Gц. Однако матрица G больше характеризует циклический код как линейный, т.к. зная расположение в ней коэффициентов Cji, сразу можно записать правило формирования проверочных символов, если циклический код рассматривать как линейный.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.